(m2 - 3m + 2)x = m - 4
Tìm giá trị nguyên của m để phương trình có nghiệm x nguyên duy nhất
Những câu hỏi liên quan
Số nguyên dương nhỏ nhất của m để phương trình (3m – 3)x + m = 3 m 2 + 1 có nghiệm duy nhất là:
A. m ≠ 1
B. m = 1
C. m = 2
D. m = 0
Cho phương trình mx-2x+3=0
a)Giải phương trình với m=-4
b)Tìm giá trị của m để phương trình có nghiệm x=2
c)Tìm giá trị của m để pt có nghiệm duy nhất
d)Tìm giá trị nguyên của m để pt có nghiệm nguyên
a, mx - 2x + 3 = 0
m = -4
<=> -4x - 2x + 3 = 0
<=> -6x = -3
<=> x = 1/2
b, mx - 2x + 3 = 0
x = 2
<=> 2m - 2.2 + 3 =0
<=> 2m - 1 = 0
<=> m = 1/2
Bài : Cho hệ phương trình (m + 1)x - y = m + 1 và x + (m -1)y = 2 ( Với m là tham số )
a: Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x - 2y = 2
b: Tìm các giá trị nguyên của m để hệ phương trình có nghiệm duy nhất (x:y) vơi x,y có giá trị nguyên
Cho hệ phương trình ( x+y = 2 mx−y = m với m là tham số.
a) Giải hệ phương trình khi m = −2.
b) Tìm giá trị của m để hệ phương trình có nghiệm duy nhất (x; y) sao cho 3x−y = −10.
c) Tìm giá trị nguyên của m để hệ phương trình có nghiệm (x; y) mà x, y là những số nguyên
a) Với m = -2
=> hpt trở thành: \(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}y=2-x\\-x=0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)
Vậy S = {0; 2}
b) Ta có: \(\left\{{}\begin{matrix}x+y=2\left(1\right)\\mx-y=m\left(2\right)\end{matrix}\right.\)
=> x + mx = 2 + m
<=> x(m + 1) = 2 + m
Để hpt có nghiệm duy nhất <=> \(m\ne-1\)
<=> x = \(\dfrac{m+2}{m+1}\) thay vào pt (1)
=> y = \(2-\dfrac{m+2}{m+1}=\dfrac{2m+2-m-2}{m+1}=\dfrac{m}{m+1}\)
Mà 3x - y = -10
=> \(3\cdot\dfrac{m+2}{m+1}-\dfrac{m}{m+1}=-10\)
<=> \(\dfrac{2m+6}{m+1}=-10\) <=> m + 3 = -5(m + 1)
<=> 6m = -8
<=> m = -4/3
c) Để hpt có nghiệm <=> m \(\ne\)-1
Do x;y \(\in\) Z <=> \(\left\{{}\begin{matrix}\dfrac{m+2}{m+1}\in Z\\\dfrac{m}{m+1}\in Z\end{matrix}\right.\)
Ta có: \(x=\dfrac{m+2}{m+1}=1+\dfrac{1}{m+1}\)
Để x nguyên <=> 1 \(⋮\)m + 1
<=> m +1 \(\in\)Ư(1) = {1; -1}
<=> m \(\in\) {0; -2}
Thay vào y :
với m = 0 => y = \(\dfrac{0}{0+1}=0\)(tm)
m = -2 => y = \(\dfrac{-2}{-2+1}=2\)(tm)
Vậy ....
Đúng 1
Bình luận (0)
Bài 6: Cho phương trình m2(x – m) x – 3m + 2 (*)a, Tìm m để (*) là phương trình bậc nhất một ẩnb, Giải PT khi m 0c, Tìm m để (1) có nghiệm x 3d, Tìm m nguyên để x nguyên
Đọc tiếp
Bài 6: Cho phương trình m2(x – m) = x – 3m + 2 (*)
a, Tìm m để (*) là phương trình bậc nhất một ẩn
b, Giải PT khi m = 0
c, Tìm m để (1) có nghiệm x = 3
d, Tìm m nguyên để x nguyên
a: =>m^2x-m^3-x+3m-2=0
=>x(m^2-1)=m^3-3m+2
=>x(m-1)(m+1)=m^3-m-2m+2=m(m-1)(m+1)-2(m-1)=(m-1)^2*(m+2)
Để đây là pt bậc nhất 1 ẩn thì (m-1)(m+1)<>0
=>m<>1 và m<>-1
b: Khi m=0 thì pt sẽ là x+2=0
=>x=-2
c: Khi x=3 thì pt sẽ là:
3(m^2-1)=m^3-3m+2
=>(m-1)^2(m+1)-3(m-1)(m+1)=0
=>(m-1)(m+1)(m-1-3)=0
=>(m-1)(m+1)(m-4)=0
=>\(m\in\left\{1;-1;4\right\}\)
Đúng 0
Bình luận (0)
Cho bất phương trình
m
2
-
x
+
12
4
-
x
2
≥
16
x
+
3
m
2
+
x
+
3
m
+
35
Có tất cả bao nhiêu giá trị nguyên của tham số
m
∈
-
10...
Đọc tiếp
Cho bất phương trình m 2 - x + 12 4 - x 2 ≥ 16 x + 3 m 2 + x + 3 m + 35 Có tất cả bao nhiêu giá trị nguyên của tham số m ∈ - 10 ; 10 để bất phương trình nghiệm đúng với mọi x ∈ - 2 ; 2 ?
A. 10
B. 18.
C. 3.
D. 4.
Cho bất phương trình
m
2
-
x
+
12
4
-
x
2
≥
16
x
+
3
m
2
+
x...
Đọc tiếp
Cho bất phương trình m 2 - x + 12 4 - x 2 ≥ 16 x + 3 m 2 + x + 3 m + 35 .Có tất cả bao nhiêu giá trị nguyên của tham số m ∈ - 10 ; 10 để bất phương trình nghiệm đúng với mọi x ∈ - 2 ; 2 ?
A. 10.
B. 18.
C. 3.
D. 4.
Chọn C
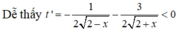
nên hàm t = t (x) nghịch biến trên (-2;2)
Thay vào bất phương trình trên được:
Bất phương trình đã cho nghiệm đúng với mọi x ∈ - 2 ; 2 nếu và chỉ nếu bất phương trình
nghiệm đúng với mọi t ∈ - 6 ; 2
tam thức bậc hai f t = 2 t 2 - m t + 3 m - 5 có hai nghiệm thỏa mãn
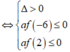
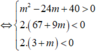
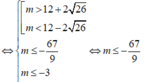
Kết hợp với m ∈ - 10 ; 10 thì m ∈ - 10 ; - 9 ; - 8
Đúng 0
Bình luận (0)
Giá trị của tham số m để phương trình
(
m
2
-
m
)
x
2
x
+
m
2
-
1
có nghiệm duy nhất x 0
Đọc tiếp
Giá trị của tham số m để phương trình ( m 2 - m ) x = 2 x + m 2 - 1 có nghiệm duy nhất x = 0
Tìm giá trị của m để hệ phương trình
x
+
y
2
m
x
−
y
m
có nghiệm nguyên duy nhất. A. m −1 B. m 0; m 1 C. m 0; m −2 D. m −2; m 1
Đọc tiếp
Tìm giá trị của m để hệ phương trình x + y = 2 m x − y = m có nghiệm nguyên duy nhất.
A. m = −1
B. m = 0; m = 1
C. m = 0; m = −2
D. m = −2; m = 1
Ta có x + y = 2 m x − y = m ⇒ x + mx = 2 + m ⇒ x(m + 1) = m + 2
Nếu m = −1 ⇒ 0.x = 1 (vô lí)
Nếu m ≠ 1 ⇒ x = m + 2 m + 1 = 1 + 1 m + 1
Để hệ phương trình đã cho có nghiệm nguyên duy nhất ⇒ x nguyên
⇒ m + 1 = ± 1 ⇒ m = 0; m = −2
Với m = 0 ⇒ x = 2 y = 0 (thỏa mãn)
Với m = −2 ⇒ x = 0 y = 2 (thỏa mãn)
Đáp án: C
Đúng 0
Bình luận (0)