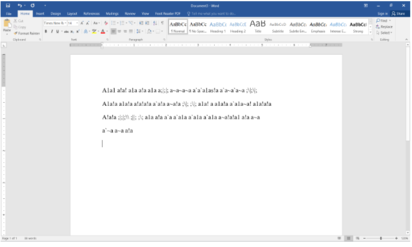
a;b>0 áp dụng bất đẳng thức 1/a + 1/b >=4/a+b .CMR 1/(a+b)+1/(b+c)+1/(a+c)>= 2(1/2a+b+c+1/a+2b+c+1/a+b+2c)
giúp mik vs
Những câu hỏi liên quan
Tập gõ các số và kí tự đặc biệt 1 ` ! \ |
A1a1 a!a! a1a a!a a1a a;|;|; a~a~a~a a`a`a1as!a a`a~a`a~a ;\|;\|;
A1a!a a1a!a a!a!a!a a`a!a a~a!a ;\|; ;\|; a1a! a a1a!a a`a1a~a! a1a!a!a
A!a!a ;|;|;\\ ;||; ;\; a1a a!a a`a a`a1a a`a1a a`a1a a~a!a!a1 a!a a~a
a`~a a~a a!a
a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+....aaaaaa+b=1
a=?
b=?
cau hoi dc day =))
Xem thêm câu trả lời
a*a*a*a*a*a*a*a+a*a*a*a*a*a*a*a=
Xem thêm câu trả lời
a^7-a=a(a^6-1)
=a(a^3+1)(a^3-1)
=a(a+1)(a^2-a+1)(a-1)(a^2+a+1)
=a(a-1)(a+1)(a^2-a+1)(a^2+a+1)
*=a(a-1) (a+1) (a^2-a+1-7) (a^2+a+1)
+7a (a-1) (a+1) (a^2+a-1)
*=a (a-1) (a+1) (a^2-a-6) (a^2+a+1-7)
+7a (a-1) (a+1) (a^2+a-1)
+7a (a-1) (a+1) (a^2-a-6)
có: 7a(a-1) (a+1) (a^2+a-1)+7a (a-1) (a+1) (a^2-a-6) chia hết cho 7
Giải thích giùm mình phần * đc k ạ.
A=a√a-1/a-√a-a√a+1/a+√a+(√a-1/√a) (√a+1/√a-1+√a-1/√a+1)
11. A. cities/s/
12. A. begged
13. A. approached
14. A. laughs
15. A. finished
16. A. expanded
17. A. expanded
18. A. promised
19. A. houses
20. A. reduced
21. A. cooked
22. A. houses
23. A. kites
24. A. attacked
25. A. possessed
26. A. derived
27. A. valued
28. A. supported
29. A. circled
30. A. matched
31. A. visited
32. A. talked
33. A. cursed
34. A. approached
11. A. cities/s/
12. A. begged d
13. A. approached t
14. A. laughs t
15. A. finished t
16. A. expanded id
17. A. expanded id
18. A. promised t
19. A. houses s
20. A. reduced s
21. A. cooked t
22. A. houses s
23. A. kites s
24. A. attacked t
25. A. possessed t
26. A. derived d
27. A. valued d
28. A. supported id
29. A. circled d
30. A. matched t
31. A. visited id
32. A. talked t
33. A. cursed t
34. A. approached t
Đúng 0
Bình luận (0)
Cho biểu thức: Aa√a−1a−√a−a√a+1a+√a+(√a-1/√a)(√a+1/√a-1 + √a-1/√a+11.rút gọn a2.tìm a để A 73.tìm a để A6
Đọc tiếp
Cho biểu thức:
1) Tìm a , biết :
a) aa = a . a = a + a
b) a - a = a + a = a . a
c) a : a = a = a . a
( Toán Vui )
a, a=0 hoặc a=2
b, b=0
c, Vì a=0 nhung a:a=0:0 không được
\(\Rightarrow\)a=1
Đúng 0
Bình luận (0)
the exam is very difficult ......... Help help help ..............thanks
1*1*11*1*1*11*1*1*1*1*11*1*1*1*1*1*1*11*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a-500=200
S = a ^1 +a^2 +a^3 +...+a^13=7. Biet a^1+a^2+a^3=a^4+a^5+a^6+a^7+a^8+a^9+a^10+a^11+a^12=5. Tinh a^13
\(S=a^1+a^2+a^3+...+a^{13}=7\)
\(\Leftrightarrow\)\(\left(a^1+a^2+a^3\right)+\left(a^4+a^5+a^6+a^7+a^8+a^9+a^{10}+a^{11}+a^{12}\right)\)\(+a^{13}=7\)
\(\Leftrightarrow\)\(5+5+a^{13}=7\)
\(\Leftrightarrow\)\(a^{13}=7-5-5=-3\)
Đúng 0
Bình luận (0)