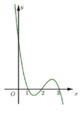
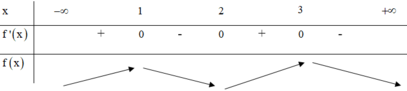
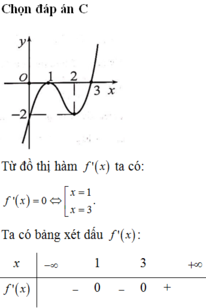Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\) và \({x_0} \in (a;b)\). Điều kiện cần và đủ để hàm số \(y = f(x)\) liên tục tại \({x_0}\) là:
A. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = f\left( {{x_0}} \right)\).
B. \(\mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).
C. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x)\).
D. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).







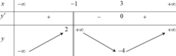
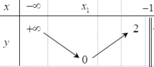

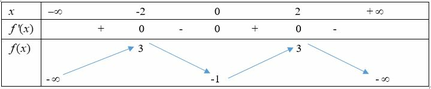

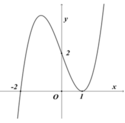

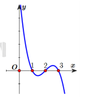 Xét các khẳng định sau:
Xét các khẳng định sau: