Đáp án A
Điều kiện đủ để hàm số y=f(x) đồng biến trên k là f ' x > 0 với mọi x ∈ K . Đáp án D thiếu tại hữu hạn điểm thuộc khoảng K.
Đáp án A
Điều kiện đủ để hàm số y=f(x) đồng biến trên k là f ' x > 0 với mọi x ∈ K . Đáp án D thiếu tại hữu hạn điểm thuộc khoảng K.
Cho K là một khoảng và hàm số y=f(x) có đạo hàm trên K. Giả sử f’(x)=0 chỉ tại một số hữu hạn điểm trên K. Khẳng định nào sau đây là đúng?
A. Nếu f ' x ≥ 0 , ∀ x ∈ K thì hàm số là hàm hằng trên K
B. Nếu f ' x > 0 , ∀ x ∈ K thì hàm số nghịch biến trên K
C. Nếu f ' x < 0 , ∀ x ∈ K thì hàm số đồng biến trên K
D. Nếu f ' x ≤ 0 , ∀ x ∈ K thì hàm số nghịch biến trên K
Cho hàm số y = f (x) có đạo hàm trên khoảng I. Xét các mệnh đề sau
(I). Nếu f’(x) ≥ 0, ∀ x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số f đồng biến trên I.
(II). Nếu f’(x) ≤ 0, ∀ x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số f nghịch biến trên I.
(III). Nếu f’(x) ≤ 0, ∀ x ∈ I thì hàm số f nghịch biến trên khoảng I.
(IV). Nếu f’(x) ≤ 0, ∀ x ∈ I và f’(x) = 0 tại vô số điểm trên I thì hàm số f không thể nghịch biến trên khoảng I.
Trong các mệnh đề trên, mệnh đề nào đúng, mệnh đề nào sai?
A. I và II đúng, còn III và IV sai
B. I, II và III đúng, còn IV sai
C. I, II và IV đúng, còn III sai
D. Cả I, II, III và IV đúng
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
![]()
![]()
![]()
![]()
Cho hàm số y = f x xác định và liên tục trên khoảng K và có đạo hàm là f’(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f’(x) trên K.
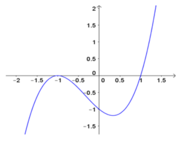
Sổ điểm cực trị của hàm số f(x) trên K là
A. 2
B. 1
C. 3
D. 0
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5
Cho hàm số có f đạo hàm trên khoảng I. Xét các mệnh đề sau:
(I). Nếu , thì hàm f '(x) < 0 "x ∈ I số nghịch biến trên I
(II). Nếu , f '(x) ≤ 0 "x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số nghịch biến trên I
(III). Nếu , thì hàm f '( x) ≤ 0 "x ∈ I số nghịch biến trên khoảng I
(IV). Nếu , f '(x) ≤ 0 "x ∈ I và f '(x) = 0 tại vô số điểm trên thì hàm I số không f thể nghịch biến trên khoảng I
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
A. I, II và IV đúng, còn III sai.
B. I, II, III và IV đúng.
C. I và II đúng, còn III và IV sai.
D. I, II và III đúng, còn IV sai.
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞