Đường tròn ( O; OA). Vé tiếp tuyến Ax. Lấy điểm B thuộc tia Ax sao cho AB= AO. Nối BO cắt đường tròn tại C. Tính số đo góc ở tâm AOC và cung lớn AC.

Những câu hỏi liên quan
cho hai đường tròn tâm O và O' tiếp xúc ngoài với nhau tại A, có đường kính AB của đường tròn tâm O, đường kính AC của đường tròn O', gọi MN là tiếp tuyến chung của hai đường tròn (M thuộc đường tròn O, N thuộc đường tròn O') hai tia BM và CN cắt nhau tại E. a) CM: tam giác EBC là tam giác vuông b) CM: EB.EM=EN.EC c) Tính MN biết bán kính của đường tròn (O) và (O') lần lượt là 9cm và 4cm
Trong nửa đường tròn tâm O đường kính AB =2R, đường tròn (I) tiếp xúc với nửa đường tròn (O) và đường kính AB. Đường tròn (K) tiếp xúc với nửa đường tròn (O) , đường tròn (I) và đường kính AB. Tính hiệu diện tích giữa đường tròn tâm I và đường tròn tâm K theo R
Cho đường tròn (O; 5cm) và điểm O' với OO' = 7cm. Vẽ đường tròn (O';R'). Với giá trị nào của R' thì đường tròn (O'; R')
a, Cắt đường tròn (O)
b, Tiếp xúc với đường tròn (O).
Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn. Đường tròn (O’) có vị trí tương đối nào với đường tròn (O) ?

Đường tròn (O’) tiếp xúc trong với đường tròn (O).
Đúng 0
Bình luận (0)
cho đường tròn (O) đường tròn AB. Vẽ một đường tròn tâm A có bán kính tùy ý cắt đường tròn (O) tại C và D. Qua B vẽ một đường thẳng cắt đường tròn tâm A tại M (điểm M nằm trong đường tròn(O)) và cắt đường tròn (O) tại N.
Chứng minh:MN^2=CN.ND
Cho đường tròn tâm O bán kính 2cm. Trên đường tròn (o) ta lấy điểm o' &vẽ đường tròn (o';2cm).hai đường tròn này cắt nhau tại hai điểm A,B.tính O,O'
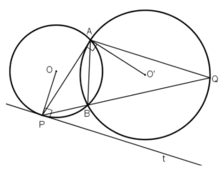
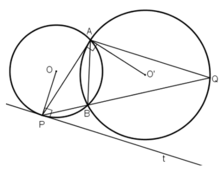
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).


Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O). Chứng minh rằng CA, CB là các tiếp tuyến của đường tròn (o’)

Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên ![]()
Suy ra: CA ⊥ O’A tại điểm A
Vậy CA là tiếp tuyến của đường tròn (O’)
Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên ![]()
Suy ra: CB ⊥ O’B tại điểm B
Vậy CB là tiếp tuyến của đường tròn (O’)
Đúng 0
Bình luận (0)
Vẽ đường tròn tâm O bán kính 2cm.Gọi M là một điểm nằm ngoài đường tròn tâm O,OM cắt đường tròn (O;2cm) ở I.Biết OM=3cm.a)Tính IM;b)Vẽ đường tròn tâm I bán kính IM.Chứng tỏ điểm O nắm ngoài đường tròn (I;IM).c)Đường tròn tâm (I;IM) cắt đường tròn (O;2cm) ở P và Q,cắt OM ở K.Chứng tỏ rắng điểm K nắm trong đường tròn (O;2cm).Vẽ hình giúp mình nha!