A K H B C Cho tam giác ABC đường cao BH;CKCMR: góc ABHACR
Đọc tiếp
Cho tam giác ABC đường cao BH;CK
CMR: góc ABH=ACR
Những câu hỏi liên quan
Cho tam giác ABC, các đường cao BH và CK. Chứng minh: Bốn điểm B, C, H, K cùng thuộc một đường tròn
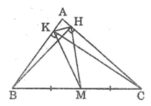
Gọi M là trung điểm của BC.
Tam giác BCH vuông tại H có HM là đường trung tuyến nên:
HM = (1/2).BC (tính chất tam giác vuông)
Tam giác BCK vuông tại K có KM là đường trung tuyến nên:
KM = (1/2).BC (tính chất tam giác vuông)
Suy ra: MB = MC = MH = MK
Vậy bốn điểm B, C, H, K cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn (AB=AC) vẽ đường cao BH , CK của tam giác (H thuộc AC, K thuộc AB )gọi E là giao điểm của BH, Ck a, chứng minh tam giác AHB đồng dạng vs tam giác AkC b, c/m kH song song vs BC
cho tam giác ABC,các đường cao BH và CK .CMR:
a, bốn điểm B,C,H,K cùng thuộc một đường tròn
b,HK<BC
Cho tam giác ABC vuông cân tại A,kẻ đường cao Mh, MK( H,K thuộc A,B)
chứng minh: AM2= BH . CK . BC
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH=4cm, CH=9cm. Gọi I và K lần lượt là hình chiếu của H lên AB và AC a. Chứng minh tứ giác AIHK là hình chữ nhật b. Cm tam giác AKI đồng dạng với tam giác ABC c. Tính diện tích của tam giác ABC
a: góc AIH=góc AKH=góc KAI=90 độ
=>AIHK là hcn
b: AIHK là hcn
=>góc AIK=góc AHK=góc C
=>ΔAIK đồng dạng với ΔACB
Đúng 0
Bình luận (0)
Cho tam giác ABC, hai đường cao BH, CK. Chứng minh:
a) 4 điểm B, K, H, C cùng thuộc 1 đường tròn
b) BK giao với CK tại I. Chứng minh 4 điểm A, H, I, K thuộc cùng 1 đường tròn
1/ Cho tam giác ABC vuông tại C , đường cao CH ( H thuộc AB ). Biết AH = 4cm , BH = 9cm
a/ Chứng minh Tam giác ABC đồng dạng tam giác CBH
b/ Chứng minh BC bình phương = BH . BA
c/ Tính diện tích Tam giác ABC
a, Xét Δ ABC và Δ CBH
Ta có : \(\widehat{ACB}=\widehat{CHB}=90^o\)
\(\widehat{ABC}=\widehat{CBH}\) (góc chung)
=> Δ ABC ∾ Δ CBH (g.g)
b, Ta có : Δ ABC ∾ Δ CBH (cmt)
=> \(\dfrac{AB}{CB}=\dfrac{BC}{BH}\)
=> \(BC^2=AB.BH\)
Đúng 1
Bình luận (0)
c,
Ta có : AB = AH + HB
=> AB = 4 + 9
=> AB = 13 (cm)
Ta có : \(BC^2=AB.BH\left(cmt\right)\)
=> \(BC^2=13.9\)
=> \(BC^2=117\)
=> BC = 10,8 (cm)
Xét Δ ABC
Ta có : \(AB^2=AC^2+BC^2\)
=> \(13^2=AC^2+10,8^2\)
=> \(169=AC^2+116,64\)
=> \(169-116,64=AC^2\)
=> \(52,36=AC^2\)
=> AC = 7,2 (cm)
Xét Δ ABC vuông tại C
=> \(S_{\Delta ABC}=\dfrac{AC.BC}{2}\)
=> \(S_{\Delta ABC}=\dfrac{7,2.10,8}{2}\)
=> \(S_{\Delta ABC}=38,88\left(cm^2\right)\)
Đúng 1
Bình luận (0)
a, Xét Δ ABC và Δ CBH
Ta có :
(góc chung)
=> Δ ABC ∾ Δ CBH (g.g)
b, Ta có : Δ ABC ∾ Δ CBH (cmt)
=> ABCB=BCBHABCB=BCBH
=> BC2=AB.BH
c,
Ta có : AB = AH + HB
=> AB = 4 + 9
=> AB = 13 (cm)
Ta có : BC2=AB.BH(cmt)BC2=AB.BH(cmt)
=> BC2=13.9BC2=13.9
=> BC2=117BC2=117
=> BC = 10,8 (cm)
Xét Δ ABC
Ta có : AB2=AC2+BC2AB2=AC2+BC2
=> 132=AC2+10,82132=AC2+10,82
=> 169=AC2+116,64169=AC2+116,64
=> 169−116,64=
=>
Đúng 1
Bình luận (0)
Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng :
a) Bốn điểm B, C, H, K cùng thuộc một đường tròn
b) HK < BC
Cho tam giác ABC ( AB = AC ), vẽ các đường cao BH, CK ( H thuộc AC, K thuộc AB )
a, CMR: BH = CK
b, CMR: KH // BC
c, Tính HK biết BC = a, AB = AC = b
Cho tam giác ABC là tam giác đều. Mỗi cạnh 5cm , đường cao BH. Trên đường thẳng BH lấy điểm K sao cho BK=5cm.
a, Tính BH
b, Tính tổng các góc ABC và AKC trong trường hợp B nằm giữa K và H
Các bạn vẽ hộ hình dùm mình luôn nhé! cảm ơn. Mình đang cần gấp