Cho tam giac ABC .Các đường trung tuyến AD;BE;CF .Các đường thẳng kẻ từ E //AB và từ F//BE cắt nhau tại G .Chứng minh
a)EG=AF
b)CG=AD
Những câu hỏi liên quan
Gọi G là trọng tam tam giac ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng: Các cạnh tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC
Cho tam giác ABC . 3 đường trung tuyến AD BE CF . Từ F kẻ đường thẳng song song với AD cắt ED tại I
a) CMR IC / / BE va CI=BE
b) Cho AD vuong goc BE CM: ICF vuông va chu vi tam giac nay bang tong do dai 3 duong trung tuyen cua tam giac ABC
cho tam giac abc co ab=c ,ac=b đường phân giac ad .đường trung tuyến am .đường tahng đối xứng với am qua ad cắt bc ở n . tính tỉ số bn:nc
Cho Tam Giac ABC có 3 đường trung tuyến AD ; BE ; CF đồng quy tại G đảo lại nếu có GD = GE =GF
Nếu Tam Giac ABC đều hãy CM GD=GE=GF
CM Tam Giac ABC đều
Cho tam giác ABC có các đường trung tuyến AM, BN, CP trọng tâm G. Gọi K là trung điểm của GB
Chứng minh rằng các cạnh của tam giác GMK bằng 1/3 các trung tuyến tam giác ABC
Nêu cách dựng tam giac ABC khi biết đọ dài 3 đường trung tuyến AM, BN, CP
Cho tam giác ABC với đường trung tuyến AD. Trên tia AD lấy điểm E sao cho AD = DE, trên tia BC lấy điểm M sao cho BC = CM. So sánh các cạnh của tam giác ABC với các đường trung tuyến của tam giác AEM
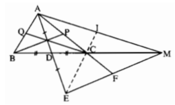
Các đường thẳng AC, EC lần lượt cắt EM, AM tại F, I. Tam giác AEM có các đường trung tuyến là AF, EI, MD. Ta có ΔADB = ΔEDC (c.g.c) nên AB = EC
Vậy: AC = 2/3 AF; BC = CM = 2/3 MD; AB = EC = 2/3 EI
Đúng 0
Bình luận (0)
Cho tam giác ABC với đường trung tuyến AD. Trên tia AD lấy điểm E sao cho AD = DE, trên tia BC lấy điểm M sao cho BC = CM. So sánh các đường trung tuyến của tam giác ABC với các cạnh của tam giác AEM.
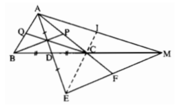
Trước tiên, theo giả thiết, ta có AD = DE nên AD = 1/2 AE
Đúng 0
Bình luận (0)
Cho tam giác ABC với đường trung tuyến AD. Trên tia AD lấy điểm E sao cho AD = DE, trên tia BC lấy điểm M sao cho BC = CM
a) Tìm trọng tâm của tam giác AEM
b) So sánh các cạnh của tam giác ABC với các đường trung tuyến của tam giác AEM
c) So sánh các đường trung tuyến của tam giác ABC với các cạnh của tam giác AEM
Giải
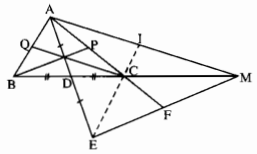
a) Do AD = DE nên MD là một đường trung tuyến của tam giác AEM. Hơn nữa do
CD=12CB=12CMCD=12CB=12CM
Nên C là trọng tâm của tam giá AEM.
b) Các đường thẳng AC, EC lần lượt cắt EM, AM tại F, I. Tam giác AEM có các đường trung tuyến là AF, EI, MD. Ta có ∆ADB = ∆EDG (c.g.c) nên AB = EC
Vậy: AC=23AF;BC=CM=23MD;AB=EC=23EIAC=23AF;BC=CM=23MD;AB=EC=23EI
c) Trước tiên, theo giả thiết, ta có AD = DE nên AD=12AEAD=12AE
Gọi BP, CQ là các trung tuyến của ∆ABC.
∆BCP = ∆MCF => BP=FM=12EMBP=FM=12EM. Ta sẽ chứng minh CQ=12AMCQ=12AM
Ta có:
ΔABD=ΔECD⇒ˆBAD=ˆCED⇒AB//EC⇒ˆQAC=ˆICAΔABD=ΔECD⇒BAD^=CED^⇒AB//EC⇒QAC^=ICA^
Hai tam giác ACQ và CAI có cạnh AC chung, ˆQAC=ˆICAQAC^=ICA^;
AQ=12AB=12EC=ICAQ=12AB=12EC=IC nên chúng bằng nhau.
Vậy CQ=AI=12AMCQ=AI=12AM.
Tóm lại: AD=12AE,BP=12EM,CQ=12AM
Đúng 0
Bình luận (0)
Cho tam giac ABC vuông tại A,AB=6cm,AC=8cm.Kẻ AH_|_BC,AD là đường trung tuyến (DthuộcBC).Tính BC,AH,HD.
BC2 = AB2 + AC2 = 36+64= 100
BC = 10cm
cac cau khac tuong tu
Đúng 0
Bình luận (0)
Cho tam giac ABC có AB=6cm ,AC=5cm tia phân giác AD đường trung tuyến qua AD cắt AC tại E tính DE