kko bbitbbits

(thầy ơi tia Om ạ ??)

vì tia Om nằm trong góc xOy

=>Om nằm giữa

mà xOy=90^o

=> xOm là góc nhọn

\(\widehat{xOm}\)  là góc nhọn

 Xét tứ giác BMOA:

+ BM // OA (b // Oy).

+ AM // OB (a // Ox).

\(\Rightarrow\) Tứ giác BMOA là hình bình hành (dhnb).

\(\Rightarrow\widehat{AMB}=\widehat{BOA}\) (Tính chất hình bình hành).

hay \(\Rightarrow\widehat{AMB}=\widehat{xOy.}\)

Ox là trung trực => OA =OB

Oy...................=> OA = OC

=> OB =OC (1)

góc BOD = COD = xOy  ( tự cm nhé) (2)

(1);(2)  => tam giác BOD =COD ( c-g-c)  ( OD chung nhé)

=> BD =CD

a

Do Ox là đường trung trực của MA nên OM=OA ( 1 ) 

Do Oy là đường trung trực của NA nên ON=OA  ( 2 )

Từ ( 1 );( 2 ) suy ra đpcm

b

Từ ( 1 ) suy ra \(\widehat{mOx}=\widehat{xOA}=\frac{1}{2}\widehat{MOA}\left(3\right)\)

Từ ( 2 ) suy ra \(\widehat{AOy}=\widehat{yON}=\frac{\widehat{AON}}{2}\left(4\right)\)

Từ ( 3 );( 4 ) suy ra \(\frac{1}{2}\left(\widehat{MOA}+\widehat{AON}\right)=\widehat{xOy}=\alpha\)

\(\Rightarrow\widehat{MON}=2\alpha\)

a) x⁴+x³+2x²+x+1=(x⁴+x³+x²)+(x²+x+1)=x²(x²+x+1)+(x²+x+1)=(x²+x+1)(x²+1)

b)a³+b³+c³-3abc=a³+3ab(a+b)+b³+c³ -(3ab(a+b)+3abc)=(a+b)³+c³-3ab(a+b+c)

=(a+b+c)((a+b)²-(a+b)c+c²)-3ab(a+b+c)=(a+b+c)(a²+2ab+b²-ac-ab+c²-3ab)=(a+b+c)(a²+b²+c²-ab-ac-bc)

c)Đặt x-y=a;y-z=b;z-x=c

a+b+c=x-y-z+z-x=o

đưa về như bài b

d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung

e)x²(y-z)+y²(z-x)+z²(x-y)=x²(y-z)-y²((y-z)+(x-y))+z²(x-y)

=x²(y-z)-y²(y-z)-y²(x-y)+z²(x-y)=(y-z)(x²-y²)-(x-y)(y²-z²)=(y-z)(x²-2y²+xy+xz+yz)

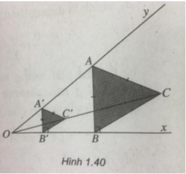
Giả sử điểm A đã dựng được . Gọi B là hình chiếu vuông góc của A trên Ox, khi đó AB = AC. Lấy điểm A' bất kì trên Oy, gọi B' là hình chiếu vuông góc của A' trên Ox, đường thẳng qua A' song song với AC cắt đường thẳng OC tại C'. Khi đó có thể coi tam giác ABC là ảnh của tam giác A'B'C' qua phép vị tự tâm O tỉ số  A C A ' C '  nên A'C' = A'B'.

Từ đó suy ra cách dựng:

- Lấy điểm A bất kì trên Oy, dựng B' là hình chiếu vuông góc của A lên Ox

- Lấy C' là một giao điểm của đường tròn tâm A' bán kính A'B' với đường thẳng OC.

- Đường thẳng qua C song song với A'C' cắt Oy tại A.

Dễ thấy A là điểm phải dựng.

Bài toán có hai nghiệm hình.