Cho tam giác ABC vuông tại A,đg cao AH,trung tuyến AM.Biết AH=40cm;AM=41cm.Tính tỉ số độ dài AB,AC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A; đường cao AH; trung tuyến AM; AH=40cm,AM=41cm. Tính tỉ số độ dài 2 cạnh góc vuông.
Cho tam giác ABC vuông tại A, AB=30cm, AC=40cm đường cao AH, trung tuyến AM. Tính độ dài BH, HM, MC, AH
BH=18 cm
MH=7 cm
MC= 25 cm
AH=24 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=30cm, AC=40cm đường cao AH, trung tuyến AM. Tính độ dài BH, HM, MC, AH
BH = 18 cm ; MH = 7 cm ; MC = 25 cm ; AH = 24 cm. Chỉ có đáp án thôi nha!
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có cạnh AB = 30cm và AC = 40cm, đường cao AH, trung tuyến AM. Tính BH, HM, MC
A. BH = 18cm; HM = 7cm; MC = 25cm
B. BH = 12cm; HM = 8cm; MC = 20cm
C. BH = 16cm; HM = 8cm; MC = 24cm
D. BH = 16cm; HM = 6cm; MC = 22cm
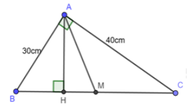
Áp dụng định lý Pytago cho ABH vuông tại A có:

Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
Vì AM là đường trung tuyến M là trung điểm BC
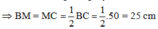
Ta có: MH = BM – BH = 25 – 18 = 7 cm
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.AB=30cm,AC=40cm,đường cao AH,trung tuyến AM,phân giác AD.
a,Tính BH,MH,MC.
b,Tính AH,AD.
c,Tính diện tích tam giác AHD và tam giác ADM.
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
nên BC=50(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AB^2=BH\cdot BC\)
hay BH=18(cm)
Ta có: ΔBAC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên \(MB=MC=\dfrac{BC}{2}=25\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM.Biết AM+AH=19,6 cm và AM-AH=0,4cm.tính diện tích tam giác ABC
https://i.imgur.com/eQreu0T.jpg
Tam giác ABC vuông tại A, đg cao AH. Từ H kể HI vuông góc với AB; HJ vuông góc với AC. Gọi AM là trung tuyến của tam giác ABC
Biết AB = 30cm; AC = 40cm. tính BC, AH, BI
Cm: IJ = AH; Am = IJ
Cm : AB x AI = AC x ẠJ; tam giác AIJ đồng dạng với tam giác ABC
Cm: tam giác ABJ và tam giác ACI đồng dạng; tam giác BI đồng dạng với tam giác IHC
Cho tam giác ABC vg ở A (AB>AC) Đg cao AH đg trung tuyến AM phân giác AD cắt đg tròn ngoại tiếp tam giác ABC lần lượt tại S,N,P.C/m MP//AH
Dễ thấy D nằm giữa M và H
Ta có : AD là tia phân giác góc BAC \(\Rightarrow\widehat{PAB}=\widehat{PAC}=\frac{1}{2}\widehat{BAC}=45^o\)
Mà \(\widehat{BAP}=\frac{1}{2}sđ\widebat{BP}=45^o\); \(\widehat{PAC}=\frac{1}{2}sđ\widebat{PC}=45^o\)
\(\Rightarrow sđ\widebat{BP}=sđ\widebat{PC}=90^o\)
Ta có : AM là đường trung tuyến nên M là tâm đường tròn ngoại tiếp tam giác ABC
\(\Rightarrow\widehat{BMP}=sđ\widebat{BP}=90^o\)
\(\Rightarrow BM\perp MP\)hay \(BC\perp MP\)( 1 )
Mà AH là đường cao tam giác ABC nên \(BC\perp AH\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra AH // MP
Tam giác ABC vuông tại A, đg cao AH. Từ H kể HI vuông góc với AB; HJ vuông góc với AC. Gọi AM là trung tuyến của tam giác ABCBiết AB 30cm; AC 40cm. tính BC, AH, BICm: IJ AH; Am IJCm : AB x AI AC x ẠJ; tam giác AIJ đồng dạng với tam giác ABCCm: tam giác ABJ và tam giác ACI đồng dạng; tam giác BI đồng dạng với tam giác IHCAi giúp mik vs mai mik phải gửi cho cô rồi !!!
Đọc tiếp
Tam giác ABC vuông tại A, đg cao AH. Từ H kể HI vuông góc với AB; HJ vuông góc với AC. Gọi AM là trung tuyến của tam giác ABC
Biết AB = 30cm; AC = 40cm. tính BC, AH, BI
Cm: IJ = AH; Am = IJ
Cm : AB x AI = AC x ẠJ; tam giác AIJ đồng dạng với tam giác ABC
Cm: tam giác ABJ và tam giác ACI đồng dạng; tam giác BI đồng dạng với tam giác IHC
Ai giúp mik vs mai mik phải gửi cho cô rồi !!!



















