Cho Δ A B C = Δ D E F . Biết rằng AB=6cm; AC=8cm, EF=10cm. Tính chu vi tam giác DEF là
A. 24cm
B. 20cm
C. 18 cm
D. 30 cm
Những câu hỏi liên quan
1 ) Cho Δ ABC , D là trung điểm của AB . Đường thẳng qua A và song song với BC cắt AC tại E , đường thẳng qua E và song song với AB cắt BC tại F . Chứng mình rằng : a ) AD EFb ) Δ ADE Δ EFCc ) AE EC2 ) Cho Δ ABC , D là trung điểm của AB , E là trung điểm của AE . Vẽ điểm F sao cho E là trung điểm của DF . Chứng minh rằng :a ) DB CFb ) Δ BDC Δ FCDc ) DE // BC và DE 1/2 BC
Đọc tiếp
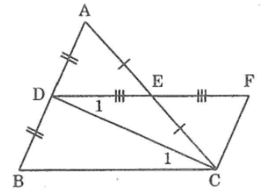
1 ) Cho Δ ABC , D là trung điểm của AB . Đường thẳng qua A và song song với BC cắt AC tại E , đường thẳng qua E và song song với AB cắt BC tại F . Chứng mình rằng :
a ) AD = EF
b ) Δ ADE = Δ EFC
c ) AE = EC
2 ) Cho Δ ABC , D là trung điểm của AB , E là trung điểm của AE . Vẽ điểm F sao cho E là trung điểm của DF . Chứng minh rằng :
a ) DB = CF
b ) Δ BDC = Δ FCD
c ) DE // BC và DE = 1/2 BC
Mình sửa lại câu hỏi của mình rồi nha bạn Hải . Bạn làm cả 2 bài giúp mình nhaaaaa
Đúng 0
Bình luận (0)
Cho Δ ABC có AB=AC. Kẻ BD vuông góc AC, CE vuông góc AB (D ϵ AC; E ϵ AB). Gọi O là giao điểm của BD và CE. Chứng minh:
a) Δ ABD = Δ ACE
b) BD = CE
c) Δ AOE = Δ AOD
d) Δ OEB = Δ ODC
e) AO là tia phân giác của góc BAC
mong mọi người giải giúp mình với ạ mình đang cần gấp
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và AC. a) Chứng minh rằng: Δ AEF Δ ABC. b) Cho AH = 4,8cm; BC = 10cm. Tính SΔAEF? c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy tại một điểm.
giúp mình câu c với ạ
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền BA, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền CA, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF\(\sim\)ΔACB
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A đường cao AH
a) chứng minh Δ ABC đồng dạng Δ BHA
b) cho AB=6cm, AC=8cm. Tính BC, AC
c) Vẽ HE vuông góc AB tại E, HF vuông góc AC tại F. Chứng minh AE.AB=AF.AC (mn giải giúp câu c vs ạ)
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
c: ΔABH vuông tại H
mà HE là đường cao
nên AE*AB=AH^2
ΔACH vuông tại H có HF là đường cao
nên AF*AC=AH^2=AE*AB
Đúng 1
Bình luận (0)
Cho tam giác MNP vuông ở M, đường cao MH, phân giác góc MNP cắt MP tại D. Cho biết MN = 6cm, MP = 8cm. a) Tính NP. Chứng minh Δ H M N và Δ H P M đồng dạng. b) Trên NP lấy điểm E sao cho PE = 4cm. Chứng minh N E 2 = N H . N P c) Tính diện tích Δ P E D
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ điểm F sao cho E là trung điểm của DF. Chứng minh rằng: Δ BDC= Δ FCD
Ta có: ΔADE= ΔCFE(chứng minh trên)
⇒∠(ADE) =∠(CFE) (hai góc tương ứng)
Suy ra: AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ΔBDC và ΔFCD, ta có:
BD = CF (chứng minh trên)
∠(BDC) =∠(FCD) (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ΔBDC= ΔFCD (c.g.c)
Đúng 0
Bình luận (0)
Bài 1: Cho Δ ABC vuông góc tại A có BC 5cm, AC 3cm, EF 3cm, DE DF 2,5cm. Chọn phát biểu đúng?A. Δ ABC ∼ Δ DEFB. ABCˆ EFDˆC. ACBˆ ADFˆD. ACBˆ DEFˆBài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ RK/PM SK/QM thì:A. Δ RSK ∼ Δ PQMB. Δ RSK ∼ Δ MPQC. Δ RSK ∼ Δ QPMD. Δ RSK ∼ Δ QMPBài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ RK/PM SK/QM thìA. RSKˆ PQMˆB. RSKˆ PMQˆC. RSKˆ MPQˆD. RSKˆ QPMˆBài 4: Chọn câu trả lời đúng?A. Δ ABC, Δ DEF;AB/DE AC/DF;Bˆ Eˆ ⇒ Δ ABC ∼ Δ DEFB. Δ ABC, Δ DEF;AB/DE AC/DF;Cˆ...
Đọc tiếp
Bài 1: Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Bài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Bài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
A. RSKˆ = PQMˆ
B. RSKˆ = PMQˆ
C. RSKˆ = MPQˆ
D. RSKˆ = QPMˆ
Bài 4: Chọn câu trả lời đúng?
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Bài 5: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5 B. 18
C. 18,5 D. 19
II. Bài tập tự luận
Bài 1: Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
tam giác abc vuông tại a, phân giác góc b cắt ac tại d, trên cạnh bc lấy e sao cho be=ba. Chứng minh :
a, Δ ABD= Δ EBD
b, DE vuông góc với BC
c, gọi F là giao điểm của ED và AB
Chứng minh ΔABC=Δ EBD
d, CM Δ ADF=Δ EDC
e, CM FC song song với AE
giúp mk với !!!!
Xét ΔABD và ΔEBD, ta có:
AB=BE ( gt)
Góc ABD= góc EBD ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD(c-g-c)
b)Vì ΔABD=ΔEBD nên góc BAD= góc BED=90 độ( 2 cạnh tương ứng)
hay DE vuông góc với BC
c) Vì ΔABD=ΔEBD nên DA=DE ( 2 cạnh tương ứng)
Xét ΔADF và ΔEDC ta có:
góc FAD=góc CED(câu b)
AD=ED (cmt)
góc ADF=gócEDC( đối đỉnh)
⇒ΔADF=ΔEDC (g-c-g)
d,Xét ΔDAE và ΔDCF có:
DA=DC
Góc ADE=góc CDF (đối đỉnh)
DE=DF
⇒ΔDAE = ΔDCF (c-g-c)
⇒góc DAE=góc DCF (2 góc tương ứng)
MÀ 2 góc này ở vị trí SLT
⇒AE//CF
Đúg thì k
Mè sai cx k hộ nhen
Cho Δ ABC vuông tại B. Tia phân giác của góc A cắt BC tại D ( D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB.
a. Chứng minh: Δ ADB = Δ ADE
B. Chứng minh: DB=DE và DE vuông góc AC
c. Trên tia AB lấy điểm F sao cho AF=AC.
Chứng minh : Ba điểm E,D,F thẳng hàng
giải thích dùm mình câu c. lun nha . cảm ơn nhiều
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE và \(\widehat{ABD}=\widehat{AED}=90^0\)
hay DE\(\perp\)AC
c: Xét ΔDBF vuông tại B và ΔDEC vuông tại E có
DB=DE
BF=EC
Do đó: ΔDBF=ΔDEC
Suy ra: \(\widehat{BDF}=\widehat{EDC}\)
=>\(\widehat{BDF}+\widehat{BDE}=180^0\)
hay F,D,E thẳng hàng
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại B. Tia phân giác của góc A cắt BC tại D ( D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB.
a. Chứng minh: Δ ADB = Δ ADE
B. Chứng minh: DB=DE và DE vuông góc AC
c. Trên tia AB lấy điểm F sao cho AF=AC.
Chứng minh : Ba điểm E,D,F thẳng hàng
giải thích dùm mình câu c. lun nha . cảm ơn nhiều
a: Xét ΔADB và ΔADE có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE và \(\widehat{ABD}=\widehat{AED}=90^0\)
hay DE\(\perp\)AC
c: Xét ΔBDF vuông tại B và ΔEDC vuông tại E có
DB=DE
BF=EC
Do đó: ΔBDF=ΔEDC
Suy ra: \(\widehat{BDF}=\widehat{EDC}\)
=>\(\widehat{BDF}+\widehat{BDE}=180^0\)
hay F,D,E thẳng hàng
Đúng 0
Bình luận (0)