cho tam giác ABC vuông ở A
Bết AB = 6 cm ; AC = 8 cm và BC = 10 cm
a. Tính chiều cao AH
b. Bết tỷ số BH/HC = 9/16 , tính diện tích tam giác ABH và ACH
Cho tam giác ABC vuông ở A đường cao ah biết AB = 6 cm biết AC = 8 cm tính số chu vi của tam giác HAC và ABC
Cho tam giác ABC có AB=6 cm ; AC = 4,5 cm : BC= 7,5 cm
a) Chứng minh tam giác ABC vuông ở A
Tính góc B ; góc C ; đường cao AH của tam giác ABC
b) Tìm tập hợp điểm M sao cho S tam giác ABC = S tam giác BMC
Bài 6:
Cho tam giác vuông ABC, vuông ở đỉnh A. Biết cạnh AB = 12 cm,
AC = 18 cm. Trên AB lấy điểm M sao cho AM = 4 cm, kẻ đường thẳng MN song song với AC cắt BC ở N. Tính độ dài MN ?
Bài 6:
Cho tam giác vuông ABC, vuông ở đỉnh A. Biết cạnh AB = 12 cm,
AC = 18 cm. Trên AB lấy điểm M sao cho AM = 4 cm, kẻ đường thẳng MN song song với AC cắt BC ở N. Tính độ dài MN ?
Cho tam giác ABC vuông ở A, có AB = 6 cm, AC = tám cm. Tìm độ dài cạnh BC
xét tam giác vuông ABC vuông tại A có :
AB2+AC2=BC2(ĐL Pi-ta-go)
mà AB=6 cm, AC=8cm
=>62+82=BC2
=>36+64= BC2
=>100=BC2
=>BC=10 cm
diện tích hình tam giác ABC là :
6*8 : 2 = 24 ( cm2 )
độ dài cạnh BC là :
24*2 : 8 = 6 ( cm )
đáp số : 6 cm
Bài 6: Cho tam giác ABC vuông tại A, AB = 4cm, AC = 3 cm, trung tuyến AD, kẻ DK vuông góc với với AB, kẻ DH vuông góc với AC
a. Tứ giác AKDH là hình gì? Vì sao?
b. Tính độ dài AD
c. Tính diện tích tam giác ABD
Bài 7: Cho ![]() ABC vuông ở A (AB < AC ), đường cao AH. Gọi D là điểm đối xứng của A qua H. Đường thẳng kẻ qua D song song với AB cắt BC và AC lần lượt ở M và N. Chứng minh:
ABC vuông ở A (AB < AC ), đường cao AH. Gọi D là điểm đối xứng của A qua H. Đường thẳng kẻ qua D song song với AB cắt BC và AC lần lượt ở M và N. Chứng minh:
a. Tứ giác ABDM là hình thoi.
b. AM ![]() CD .
CD .
c. Gọi I là trung điểm của MC; chứng minh IN ![]() HN.
HN.
Bài 6:
a: Xét tứ giác AKDH có
\(\widehat{AKD}=\widehat{AHD}=\widehat{KAH}=90^0\)
Do đó: AKDH là hình chữ nhật
b: Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên AD=BC/2=2,5(cm)
a. Tứ giác AKDH là hình chữ nhật , vì có góc \(DKA=KAH=DHA=90^o\)
b, áp dụng đl pytago vào tam giác vuông ABC có :
\(BC^2=AB^2+AC^2\Leftrightarrow BC=\sqrt{4^2+3^2}=5cm\)
vì AD là trung tuyến tam giác vuông ABC nên :
\(AD=\dfrac{1}{2}BC=\dfrac{1}{2}.5=2,5cm\)
c,vì AKDH là hình chữ nhật nên : DH//KA
mà D là trung điểm BC
=>H là trung điểm AC
<=>AH=\(\dfrac{1}{2}AC=\dfrac{1}{2}.3=1,5cm\)
vì AH = 1,5 cm nên => KD cũng = 1,5cm (AKDH là hình chữ nhật)
\(S_{ABD}=\dfrac{1}{2}.AB.KD=\dfrac{1}{2}.4.1,5=3cm^2\)
Cho tam giác ABC vuông ở A có AB = 6 cm AC = 8 cm Vẽ đường cao AH AC tính BC b Chứng minh tam giác ABC đồng dạng tam giác ahb c a chứng minh AB vuông bằng BH nhân BC nhân tính bh , b c đi Vẽ phân giác AD của góc A D thuộc BC Tính dB
a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
c: BA/BH=BC/BA
=>BA^2=BH*BC
Cho tam giác ABC có số đo cạnh BC = 32 cm bết nếu kéo dài đoạn BC thêm 4 cm thì diện tích tam giác sẽ tăng thêm 54cm vuông . Hỏi tam giác ABC có diện tích bằng bao nhiêu ?
Chiều cao là :
54 x 2 : 4 = 27 ( cm )
Diện tích tam giác ABC là :
32 x 27 : 2 = 432 ( cm2 )
Đáp số : 432 cm2
Cho tam giác ABC ( vuông ở A ) . Có AB = 30 cm, AC = 40 cm ,BC = 50 cm . D và E trên AB và AC . Cho biết diện tích hình thang BDEC có chiều cao là 6 cm
a, Hãy tính 3 đường cao tam giác ABC
b,Tính diện tích tam giác ADE
Bài 2. 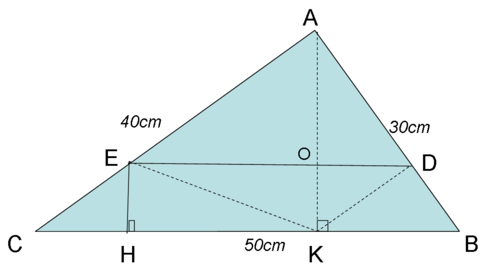
a) Trong tam giác vuông thì 2 cạnh góc vuông cũng chính là 2 đường cao của tam giác đó.
Vậy đường cao AB = 30 cm ; đường cao AC = 40 cm
Đường cao tam giác ABC còn lại đỉnh A là : 30 x 40 : 50 = 24 (cm)
b) S_ECK + S_DKB = CK x 6 : 2 + KB x 6 : 2 = (CK+KB) x 6 : 2 = 50 x 3 = 150 (cm2)
S_AEKD = 30 x 40 : 2 - 150 = 450 (cm2)
Xét tam giác AED và EDK chung đáy ED chiều cao AO = 24 - 6 = 18 (cm)
Tỉ lệ AO/OK = 18/6 = 3. Vậy S_AED = 3 x S_EDK
Diện tích tam giác AED là : 450 : (1+3) x 3 = 337,5 (cm2)
WTF!!!!!!!!!! Khó Zậy!!!
Cho tam giác ABC vuông ở A ,đường cao AH , có AB = 6 cm , AC = 8 cm a.tính độ dài cạnh BC b.Chứng minh hai tam giác HAB và HCA đồng dạng c.Lấy điểm E trên cạnh BC sao cho CE = 4cm.Chứng Minh BE2=BH.BC d.Tia phân giác của góc ABC cắt cạnh AC ở D . Tính DIện Tích Tam Giác CED Làm Phiền Mọi Người Ạ
a) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
b) Xét \(\Delta HAB\) và \(\Delta HCA\) có:
\(\widehat{AHB}=\widehat{AHC}=90^0\)
\(\widehat{HAB}=\widehat{HCA}\) (cùng phụ với \(\widehat{B}\))
\(\Rightarrow\Delta HAB\sim\Delta HCA\) (g.g)
c) Em kiểm tra lại đề bài nhé.