Cho tam giác ABC có BD là đường phân giác . Tính độ dài cạnh Ac nếu biết AB : BC =2;7 và DC -DA=1cm
mong trả lời nhanh dùm em ạ
Những câu hỏi liên quan
1. cho tam giác abc vuông a có cạnh ab6cm, bc10cm.các đường phân giác trong và ngoài của góc b cắt ac lần lượt ở d và e. tính các đoạn thẳng bd và be2. cho tam giác abc vuông ở a, phân giác ad,đường cao ah. biết cd68cm, bd51cm. tính bh,hc3. cho tam giác abc có góc b60 độ, ac13cm và bc-ba7cm. tính độ dài các cạnh ab,bc4. cho tam giác abc cân ở b và điểm d trên cạnh ac. biết góc bdc60 độ, ad3dm, dc8dm. tính ab
Đọc tiếp
1. cho tam giác abc vuông a có cạnh ab=6cm, bc=10cm.các đường phân giác trong và ngoài của góc b cắt ac lần lượt ở d và e. tính các đoạn thẳng bd và be
2. cho tam giác abc vuông ở a, phân giác ad,đường cao ah. biết cd=68cm, bd=51cm. tính bh,hc
3. cho tam giác abc có góc b=60 độ, ac=13cm và bc-ba=7cm. tính độ dài các cạnh ab,bc
4. cho tam giác abc cân ở b và điểm d trên cạnh ac. biết góc bdc=60 độ, ad=3dm, dc=8dm. tính ab
Cho tam giác ABC (AB < AC), đường phân giác của góc A cắt cạnh BC tại D. Gọi H và K lần lượt là hình chiếu của B, C lên đường phân giác AD. a/Tính độ dài cạnh BC nếu biết AB=14 cm,ac=21cm,bd=8cm b/chứng minh: DHDK=BHCK=ABAC
Bài 1c) Cho tam giác ABC cân tại A, phân giác BD. Biết góc BAC120 độ. Tính các cạnh của tam giácBài 2: Cho tam giác ABC cân ở A, BC8cm, phân giác của góc B cắt đường cao AH ở K, AK/AH3/5. a) Tính độ dài AB (câu này tớ làm đc rồi)b) Đường thẳng vuông góc với BK tại B cắt AH ở E. Tính EH (còn mỗi câu này thôi)Bài 3: Cho tam giác ABC cân, có BABCa, ACb. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại Na) Cm: MN//AC b) Tính MN theo a,bBài 4: Cho tam giác ABC cân ở A, phân giác t...
Đọc tiếp
Bài 1c) Cho tam giác ABC cân tại A, phân giác BD. Biết góc BAC=120 độ. Tính các cạnh của tam giác
Bài 2: Cho tam giác ABC cân ở A, BC=8cm, phân giác của góc B cắt đường cao AH ở K, AK/AH=3/5.
a) Tính độ dài AB (câu này tớ làm đc rồi)
b) Đường thẳng vuông góc với BK tại B cắt AH ở E. Tính EH (còn mỗi câu này thôi)
Bài 3: Cho tam giác ABC cân, có BA=BC=a, AC=b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N
a) Cm: MN//AC
b) Tính MN theo a,b
Bài 4: Cho tam giác ABC cân ở A, phân giác trong BD, BC=10cm, AB=15cm
a) Tính AD, DC
b) Đường phân giác ngoài góc B của tam giác ABC cắt đường thẳng AC tại D'. Tính D'C
Bài 5: Cho tam giác ABC có AB=5cm, AC=6cm, BC=7cm. Gọi G là trọng tâm tam giác ABC, O là giao điểm của 2 đường phân giác BD, AE
a) Tính độ dài đoạn thẳng AD
b) Cm: OG//AC
HD: a) AD=2,5cm b) OG//DM => OG//AC
Bài 6: Cho tam giác ABC. Gọi I là trung điểm của cạnh BC. Đường phân giác của góc AIB cắt cạnh AB ở M. Đường phân giác của góc AIC cắt cạnh AC ở N
a) CMR: MN//BC
b) Gọi giao điểm của DE và AM là O. CM: OM=ON
c) Tam giác ABC phải thoả mãn điều kiện gì để có MN=AI
d) Tam giác ABC phải thoả mãn điều kiện gì để có MN vuông góc với AI
Cho tam giác ABC có góc B bằng 120 ° , BC = 12cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D. Tính độ dài đường phân giác BD
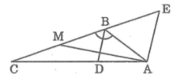
Suy ra tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A coa AB=AC=5cm đường phân giác BD(D thuộc AC ) . kẻ DH vuông góc với BC tại H .a) tính độ dài cạnh BC b) chứng minh tam giác ABD = tam giác HBD và BD là đường trung trực của AH c) trên cạnh AB lấy E sao cho AC=AD . đường vuông góc với BD kẻ từ E cắt BC ở G . chứng minh GH=HC
cho tam giác ABC vuông tại A có AB = 6cm AC = 8cm
a) tính độ dài cạnh BC
b) vẽ tia phân giác BD của góc ABC ( D thuộc AC ) từ D vẽ DE vuông góc với BC ( E thuộc BC ) chứng minh tam giác ABD=tam giác EBD
c)chứng minh BD là đường trung trực của đoạn thẳng FC
Các bạn chỉ cần làm giúp mình câu 3 thôi nhé
a) Xét △ABC vuông tại A có:
BC² = AC² + AB² (ĐL Pytago)
BC² = 8² + 6²
BC² = 100
BC = 10 cm
Vậy BC = 10 cm
b) Xét △ABD và △EBD có:
góc BAD = góc BED (=90°)
BD chung
góc ABD = góc EBD (BD là tia p/g của góc ABC)
=> △ABD = △EBD (ch-gn)
c) Câu này đề bài có cho thiếu gia thiết ko bạn chứ vẽ hình chả biết ntn á
Đúng 2
Bình luận (0)
a) Xét △ABC vuông tại A có:
BC² = AC² + AB² (ĐL Pytago)
BC² = 8² + 6²
BC² = 100
BC = 10 cm
Vậy BC = 10 cm
b) Xét △ABD và △EBD có:
góc BAD = góc BED (=90°)
BD chung
góc ABD = góc EBD (BD là tia p/g của góc ABC)
=> △ABD = △EBD (ch-gn)
cre baji
Đúng 0
Bình luận (0)
BÀI 1: Tam giác ABC vuông tại A, ĐƯỜNG PHÂN GIÁC bd. Tính AB,AC biết rằng AD4cm, DC5 cmBài 2: Tam giác ABC có AB30cm, AC45cm, BC50cm, đương phân giác BDa)Tính BD, BCb)Qua D vẽ DE//AB,DF//AC, E và F thuộc AC và AB. Tính các cạnh của tứ giác AEDFBìa 3: Tam giác ABC vuông tại A, AB 36cm, AC 48cm, đường phân giác AK. Tia phân giác của góc B cắt AK tại I. Qua I kẻ đường thẳng song song với BC cắt AB ở D, cắt AC ở E.a)Tính độ dài BKb)Tính tỉ số AI/AKc) Tính độ dài DE
Đọc tiếp
BÀI 1: Tam giác ABC vuông tại A, ĐƯỜNG PHÂN GIÁC bd. Tính AB,AC biết rằng AD=4cm, DC=5 cm
Bài 2: Tam giác ABC có AB=30cm, AC=45cm, BC=50cm, đương phân giác BD
a)Tính BD, BC
b)Qua D vẽ DE//AB,DF//AC, E và F thuộc AC và AB. Tính các cạnh của tứ giác AEDF
Bìa 3: Tam giác ABC vuông tại A, AB =36cm, AC= 48cm, đường phân giác AK. Tia phân giác của góc B cắt AK tại I. Qua I kẻ đường thẳng song song với BC cắt AB ở D, cắt AC ở E.
a)Tính độ dài BK
b)Tính tỉ số AI/AK
c) Tính độ dài DE
Cho tam giác ABC vuông tại A với đường phân giác trong AD (Dnằm trên cạnh BC). Biết AB 3cm AC 4cm. Tính độ dài đoạn thẳng BD.
Đọc tiếp
Cho tam giác ABC vuông tại A với đường phân giác trong AD (Dnằm trên cạnh BC). Biết AB 3cm AC 4cm. Tính độ dài đoạn thẳng BD.
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Xét ΔABC có
AD là đường phân giác trong ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{BC}{7}=\dfrac{5}{7}\)
Do đó: \(\dfrac{BD}{3}=\dfrac{5}{7}\)
hay \(BD=\dfrac{15}{7}cm\)
Vậy: \(BD=\dfrac{15}{7}cm\)
Đúng 1
Bình luận (1)
bài 1 Cho tam giác ABC đường phân giác của góc BAC cắt BC ở M biết BM 15 , CM 10 . Qua M //AB cắt AC tại E . Tính AE , Ec , ME biết AC 20bài 2 Cho Tam giác ABC có chu vi bằng 27 , BC là cạnh lớn nhất của AB , đường phân giác góc B chia cạnh thành 2 phần bằng nhau tỉ lệ với 1/2 . Đường phân giác của góc C chia cạnh AB thành 2 đoạn thẳng tỉ lệ 4:3 . tính độ dài các cạch của tam giác ABCbài 3 Cho tam giác ABC có AB6 , AC 9 , BC7,5 , đường phân giác trong và ngoài của goác A cắt BC theo thứ tự ở D...
Đọc tiếp
bài 1 Cho tam giác ABC đường phân giác của góc BAC cắt BC ở M biết BM =15 , CM =10 . Qua M //AB cắt AC tại E . Tính AE , Ec , ME biết AC =20
bài 2 Cho Tam giác ABC có chu vi bằng 27 , BC là cạnh lớn nhất của AB , đường phân giác góc B chia cạnh thành 2 phần bằng nhau tỉ lệ với 1/2 . Đường phân giác của góc C chia cạnh AB thành 2 đoạn thẳng tỉ lệ 4:3 . tính độ dài các cạch của tam giác ABC
bài 3 Cho tam giác ABC có AB=6 , AC= 9 , BC=7,5 , đường phân giác trong và ngoài của goác A cắt BC theo thứ tự ở D và E . Tính BD , BE , ED
giúp mình với tối đi học rồi