cho điểm A thuộc đường tròn (O;3cm).Trên tiếp tuyến tại A của đường tròn (O) lấy điểm B sao cho AB=4cm.Tính độ dài đoạn thẳng OB
ai cứu mik với mik đang cần gấp;.;

Những câu hỏi liên quan
Cho đường tròn (O), A là một điểm bất kì thuộc đường tròn. Vẽ A’ đối xứng với A qua O (h.56). Chứng minh rằng điểm A’ cũng thuộc đường tròn (O).
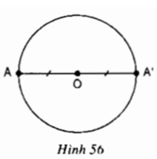
Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O), A là một điểm bất kì thuộc đường tròn. Vẽ A’ đối xứng với A qua O (h.56). Chứng minh rằng điểm A’ cũng thuộc đường tròn (O).
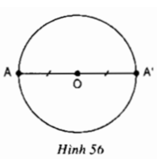
Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
cho điểm A thuộc đường thẳng a. trên đường thẳng vuông góc với a tại A, lấy diểm O sao cho OA 5cm. Vẽ đường tròn (O;3cm). M là điểm bất kỳ trên a, vẽ tiếp tuyến MB với đường tròn (O) (B là tiếp điểm). Vẽ dây BC của đường tròn (O) vuông góc với OM, cắt OM tại N.a) đường thẳng a có vị trí như thế nào với đường tròn (O)? vì sao?b) cm MC là tiếp tuyến của đường tròn (O).c) cm bốn điểm A,B,O,M cùng thuộc một đường tròn.
Đọc tiếp
cho điểm A thuộc đường thẳng a. trên đường thẳng vuông góc với a tại A, lấy diểm O sao cho OA= 5cm. Vẽ đường tròn (O;3cm). M là điểm bất kỳ trên a, vẽ tiếp tuyến MB với đường tròn (O) (B là tiếp điểm). Vẽ dây BC của đường tròn (O) vuông góc với OM, cắt OM tại N.
a) đường thẳng a có vị trí như thế nào với đường tròn (O)? vì sao?
b) cm MC là tiếp tuyến của đường tròn (O).
c) cm bốn điểm A,B,O,M cùng thuộc một đường tròn.
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A kẻ các đường AB, AC lần lượt vuông góc với OB, OC (B,C thuộc đường tròn). Vẽ đường kính BD của đường trên (O), AD cắt (O) tại E. Gọi H là giao điểm của OA và BC.
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD 2OH
Đọc tiếp
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A kẻ các đường AB, AC lần lượt vuông góc với OB, OC (B,C thuộc đường tròn). Vẽ đường kính BD của đường trên (O), AD cắt (O) tại E. Gọi H là giao điểm của OA và BC.
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD = 2OH
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD = 2OH
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Dùng thước và compa, hãy dựng các điểm B và C thuộc đường tròn (O) sao cho AB và AC là các tiếp tuyến của đường tròn (O).
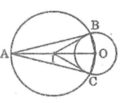
* Phân tích
Giả sử tiếp tuyến AB và AC cần dựng thỏa mãn điều kiện bài toán
Ta có: AB ⊥ OB ⇒ ∠ ABO = 90 °
AC ⊥ OC ⇒ ∠ ACO = 90 °
Tam giác ABO có ∠ ABO = 90 ° nội tiếp trong đường tròn đường kính AO và tam giác ACO có ∠ ACO = 90o nội tiếp trong đường tròn đường kính AO.
Suy ra B và C là giao điểm của đường tròn đường kính AO với đường tròn (O).
* Cách dựng
- Dựng I là trung điểm của OA
- Dựng đường tròn (I; IO) cắt đường tròn (O) tại B và C
- Nối AB, AC ta được hai tiếp tuyến cần dựng
* Chứng minh
Tam giác ABO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ABO = 90 °
Suy ra: AB ⊥ OB tại B nên AB là tiếp tuyến của đường tròn (O)
Tam giác ACO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ACO = 90 °
Suy ra: AC ⊥ OC tại C nên AC là tiếp tuyến của đường tròn (O)
* Biện luận
Luôn dựng được đường tròn tâm I, cắt đường tròn tâm O tại hai điểm B và C và luôn có AB, AC là hai tiếp tuyến của đường tròn (O).
Đúng 0
Bình luận (0)
Cho đường tròn (O;R), đường kính AB. Lấy điểm C thuộc đường tròn (O;R) sao cho AC BC. Kẻ đường cao CH của tam giác ABC (H thuộc AB), kéo dài CH cắt (O;R) tại điểm D (D C). Tiếp tuyến tại điểm A và tiếp tuyến tại điểm C của đường tròn (O;R) cắt nhau tại điểm M. Gọi I là giao điểm của OM và AC. a) Chứng minh bốn điểm M,A,O,C cùng thuộc đường tròn đường kính OM b) Hai đường thẳng MC và AB cắt nhau tại F. Chứng minh BC 2.IO và DF là tiếp tuyến của (O;R). c) Chứng minh AF.BH BF.AH.
Đọc tiếp
Cho đường tròn (O;R), đường kính AB. Lấy điểm C thuộc đường tròn (O;R) sao cho AC > BC. Kẻ đường cao CH của tam giác ABC (H thuộc AB), kéo dài CH cắt (O;R) tại điểm D (D = C). Tiếp tuyến tại điểm A và tiếp tuyến tại điểm C của đường tròn (O;R) cắt nhau tại điểm M. Gọi I là giao điểm của OM và AC. a) Chứng minh bốn điểm M,A,O,C cùng thuộc đường tròn đường kính OM b) Hai đường thẳng MC và AB cắt nhau tại F. Chứng minh BC = 2.IO và DF là tiếp tuyến của (O;R). c) Chứng minh AF.BH = BF.AH.
Cho đường tròn (O;R),đường kính AB . Qua điểm A kẻ tiếp tuyến Ax đến đường tròn (O) . Trên tia Ax lấy điểm C sao cho AC > R . Từ điểm C kẻ tiếp tuyến CM với đường tròn (O) (M là tiếp điểm)
a) Chứng minh 4 điểm A,C,O,M cùng thuộc một đường tròn
b) Chứng minh rằng MB//OC
c) Gọi K là giao điểm thứ hai của BC với đường tròn (O) . Chứng minh rằng BC.BK`=4R^2`
a: Xét tứ giác OACM có
\(\widehat{OAC}+\widehat{OMC}=90^0+90^0=180^0\)
=>OACM là tứ giác nội tiếp
=>O,A,C,M cùng thuộc một đường tròn
b: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM
=>C nằm trên đường trung trực của AM(1)
OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
=>OC\(\perp\)AM
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM\(\perp\)MB tại M
Ta có: AM\(\perp\)MB
AM\(\perp\)OC
Do đó: OC//MB
c: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
=>KB\(\perp\)KA tại K
=>AK\(\perp\)BC tại K
Xét ΔABC vuông tại A có AK là đường cao
nên \(BK\cdot BC=BA^2=\left(2R\right)^2=4R^2\)
Đúng 1
Bình luận (0)
Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn (O; R)
B. Điểm M nằm trên đường tròn (O; R)
C.Điểm M nằm trong đường tròn (O; R)
D. Điểm M không thuộc đường tròn (O; R)
Cho đường tròn (O; R) đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O). Trên tia Ax lấy điểm E khác A. Vẽ tiếp tuyến EC với đường tròn (O) (E là tiếp điểm, C khác A).
a) CM: 4 điểm A, E, C, O cùng thuộc một đường tròn.
b) Gọi K là trung điểm của BC. Tia OK cắt tia EC tại F. Chứng minh BF là tiếp tuyến của đường tròn (O).
c) Gọi H là giao điểm của AC và OE. Chứng minh AB^24OH.OE
Đọc tiếp
Cho đường tròn (O; R) đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O). Trên tia Ax lấy điểm E khác A. Vẽ tiếp tuyến EC với đường tròn (O) (E là tiếp điểm, C khác A).
a) CM: 4 điểm A, E, C, O cùng thuộc một đường tròn.
b) Gọi K là trung điểm của BC. Tia OK cắt tia EC tại F. Chứng minh BF là tiếp tuyến của đường tròn (O).
c) Gọi H là giao điểm của AC và OE. Chứng minh \(AB^2=4OH.OE\)
Cho đường tròn (O). Đường thẳng (d) không đi qua tâm (O) cắt đường tròn tại hai điểm A và B theo thứ tự, C là điểm thuộc (d) ở ngoài đường tròn (O). Vẽ đường kính PQ vuông góc với dây AB tại D ( P thuộc cung lớn AB), Tia CP cắt đường tròn (O) tại điểm thứ hai là I, AB cắt IQ tại K.a) Chứng minh tứ giác PDKI nội tiếp đường tròn.b) Chứng minh CI.CP CK.CDc) Chứng minh IC là phân giác của góc ngoài ở đỉnh I của tam giác AIB.d) Cho ba điểm A, B, C cố định. Đường tròn (O) thay đổi...
Đọc tiếp
Cho đường tròn (O). Đường thẳng (d) không đi qua tâm (O) cắt đường tròn tại hai điểm A và B theo thứ tự, C là điểm thuộc (d) ở ngoài đường tròn (O). Vẽ đường kính PQ vuông góc với dây AB tại D ( P thuộc cung lớn AB), Tia CP cắt đường tròn (O) tại điểm thứ hai là I, AB cắt IQ tại K.
a) Chứng minh tứ giác PDKI nội tiếp đường tròn.
b) Chứng minh CI.CP = CK.CD
c) Chứng minh IC là phân giác của góc ngoài ở đỉnh I của tam giác AIB.
d) Cho ba điểm A, B, C cố định. Đường tròn (O) thay đổi nhưng vẫn đi qua A và B. Chứng minh rằng IQ luôn đi qua một điểm cố định.
a) Tứ giác PDKI nọi tiếp đườngtròn đường kính PK.
b) Ta có \(\Delta CIK\sim\Delta CDP(g.g)\) nên \(CI.CP=CK.CD\).
c) Giả sử Q nằm trên cung nhỏ AB.
Khi đó Q là điểm chính giữa của cung nhỏ AB nên IQ là phân giác của góc AIB. Lại có IC vuông góc với IQ nên IC là phân giác ngoài của tam giác IAB.
b) Theo phương tích ta có CP . CI = CA . CB.
Lại có CK . CD = CI . CP nên CK . CD = CA . CB.
Mà C, A, B cố định và D là trung điểm của AB \(\Rightarrow\) D cố định nên K cũng cố định.
Vậy QI đi qua K cố định.
Đúng 1
Bình luận (0)



















