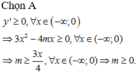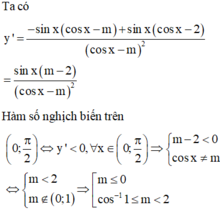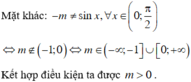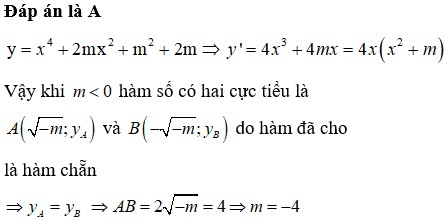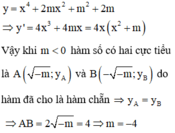Tìm tất cả các giá trị thực của tham số m để khoảng cách từ điểm M (0;3) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y= x^3 + 3mx +1 bằng \(\dfrac{2}{\sqrt{5}}\)

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số \(m\) để khoảng cách từ điểm \(M\left(0;3\right)\) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \(y=x^3+3mx+1\) bằng \(\dfrac{2}{\sqrt{5}}\)
Ta có : \(y'=3x^2+3m\)
Điều kiện để hàm số có 2 điểm cực trị là y'=0 có 2 nghiệm phân biệt
\(\Leftrightarrow 3x^2=-3m\) có 2 nghiệm phân biệt
\(\Leftrightarrow m<0\)
Đường thẳng đi qua 2 điểm cực trị là phần dư khi lấy y chia cho y':
\(x^3+3mx+1=\dfrac{x}{3}.(3x^2+3m)+2mx+1\)
\(=>\) đường thẳng đi qua 2 điểm cực trị có dạng: \(y=2mx+1\)
\(\Leftrightarrow 2mx-y+1=0\) \((\Delta)\)
\(d_{(M,\Delta)}=\dfrac{|0.2m+3.(-1)+1|}{\sqrt{4m^2+1}}=\dfrac{2}{\sqrt{5}}\)
\(\Leftrightarrow 4m^2+1=5 \Leftrightarrow m^2=1 \Leftrightarrow m=\pm1\)
Đối chiếu với điều kiện ta được \(m=1\)
Đúng 3
Bình luận (1)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
3
(
m
2
-
1
)
x
-...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
![]()
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
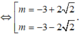
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
2
m
x
2
+
m
đồng biến trên khoảng
(
-
∞
;
0
)
A. B. C. Khô...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 2 m x 2 + m đồng biến trên khoảng ( - ∞ ; 0 )
A.![]()
B. ![]()
C. Không có m
D. Mọi ![]()
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
2
m
x
2
+
m
đồng biến trên khoảng
-
∞
;
0
A.
m
≥
0
B.
m
≤
0
C. Không có m D. Mọi
m
∈
R
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 2 m x 2 + m đồng biến trên khoảng - ∞ ; 0
A. m ≥ 0
B. m ≤ 0
C. Không có m
D. Mọi m ∈ R
Tìm tất cả các giá trị thực của tham số m để hàm số
y
cos
x
−
2
cos
x
−
m
nghịch biến trên khoảng
0
;
π
2
A. m 2 B.
m
≤
0
hoặc
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = cos x − 2 cos x − m nghịch biến trên khoảng 0 ; π 2
A. m > 2
B. m ≤ 0 hoặc 1 ≤ m < 2
C. m ≤ 2
D. m ≤ 0
Tìm tất cả các giá trị thực của tham số m để hàm số
y
sinx
−
m
sinx
+
m
đồng biến trong khoảng
0
;
π
2
. A.
m
≥
0
B.
m
0
C. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = sinx − m sinx + m đồng biến trong khoảng 0 ; π 2 .
A. m ≥ 0
B. m > 0
C. − ∞ ; − 1 ∪ 0 ; + ∞
D. − ∞ ; − 1 ∪ 0 ; + ∞
Tìm tất cả các giá trị thực của tham số m để hàm số
y
cos
x
-
2
cos
x
-
m
đồng biến trên khoảng (0;
π
2
). A.. B.. C. hoặc . D..
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = cos x - 2 cos x - m đồng biến trên khoảng (0; π 2 ).
A.![]() .
.
B.![]() .
.
C.![]() hoặc
hoặc ![]() .
.
D.![]() .
.
Chọn D
Đặt ![]() ,
, ![]() thì
thì ![]() . Ta có:
. Ta có:
![]()
![]()
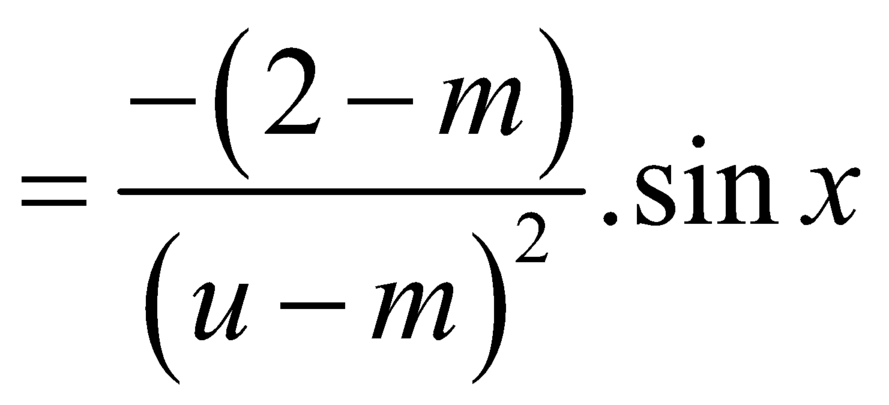 .
.
Vì ![]() nên ycbt
nên ycbt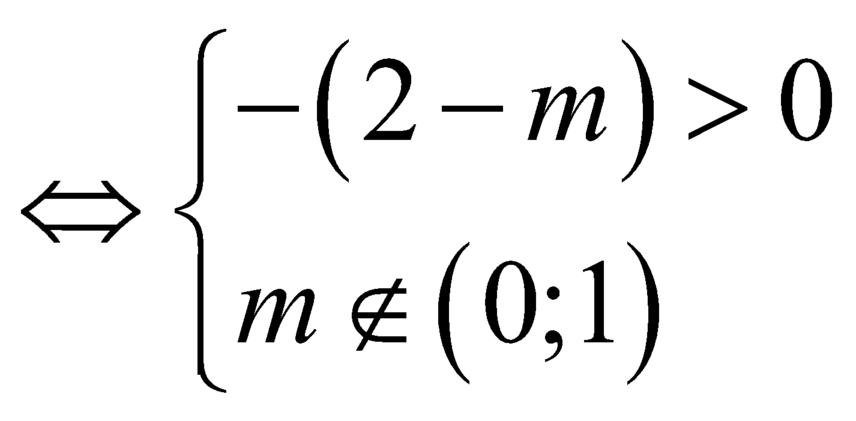 .
.
Đến đây giải được: ![]() .
.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
+
(
m
+
3
)
x
2
-
(
2
m
+
9
)
x
+
m
+
6
có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để (C) có hai điểm cực trị và khoảng cách từ gốc toạ độ O đến đường thẳng nối hai điểm cực trị là lớn nhất. A. m
-...
Đọc tiếp
Cho hàm số y = x 3 + ( m + 3 ) x 2 - ( 2 m + 9 ) x + m + 6 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để (C) có hai điểm cực trị và khoảng cách từ gốc toạ độ O đến đường thẳng nối hai điểm cực trị là lớn nhất.
A. m = - 6 ± 3 2 2
B. m = - 3 ± 3 2 2
C. m = - 3 ± 6 2
D. m = - 6 ± 6 2
Tìm tất cả các giá trị thực của tham số m để sao cho đồ thị của hàm số y = x 4 + 2 m x 2 + m 2 + 2 m có ba điểm cực trị và khoảng cách giữa hai điểm cực tiểu bằng 4.
A. m=-4
B. m=5
C. m=1
C. m=3
Tìm tất cả các giá trị thực của tham số m để sao cho đồ thị của hàm số
y
x
4
+
2
mx
2
+
m
2
+
2
m
có ba điểm cực trị và khoảng cách giữa hai điểm cực tiểu bằng 4. A. m -4 B. m 5 C.
m
1
2
D. m 3
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để sao cho đồ thị của hàm số y = x 4 + 2 mx 2 + m 2 + 2 m có ba điểm cực trị và khoảng cách giữa hai điểm cực tiểu bằng 4.
A. m = -4
B. m = 5
C. m = 1 2
D. m = 3