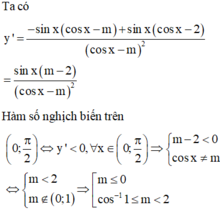Các câu hỏi tương tự
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số
y
m
cos
x
+
1
cos
x
+
m
đồng biến trên khoảng
0
;
π
3
A. ...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = m cos x + 1 cos x + m đồng biến trên khoảng 0 ; π 3
A. - 1 ; 1
B. - ∞ ; - 1 ∪ 1 ; + ∞
C. [ - 1 ; - 1 2 )
D. - 1 ; - 1 2
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
x
−
1
x
−
m
nghịch biến trên khoảng
−
∞
;
2
. A.
1
,
+
∞
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x − 1 x − m nghịch biến trên khoảng − ∞ ; 2 .
A. 1 , + ∞
B. 2 , + ∞
C. 2 , + ∞
D. 1 , + ∞
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
+
2
-
m
x
+
1
nghịch biến trên các khoảng mà nó xác định? A.
m
≤
1
....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên các khoảng mà nó xác định?
A. m ≤ 1 .
B.m<1
C.m<-3
D. m ≤ - 3 .
Tìm tất cả các giá trị thực của tham số m để hàm số
y
-
x
3
+
2
x
2
-
m
-
1
x
+
2
nghịch biến trên khoảng
-
∞
;
+
∞
A.
m
≤
7...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 2 x 2 - m - 1 x + 2 nghịch biến trên khoảng - ∞ ; + ∞
A. m ≤ 7 3
B. m ≥ 7 3
C. m ≥ 1 3
D. m > 7 3
Cho hàm số f(x)3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
mf
2
(
x
)
+
3
(
m...
Đọc tiếp
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
m
x
+
2
m
+
1
x
-
m
nghịch biến trên khoảng
0
;
+
∞
A.
m
∈
0
;...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 2 m + 1 x - m nghịch biến trên khoảng 0 ; + ∞
A. m ∈ 0 ; + ∞
B. m ∈ ( - ∞ ; 0 ] \ - 1
C. m ∈ R \ - 1
D. m ∈ R
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
mx
+
2
m
+
1
x
−
m
nghịch biến trên khoảng
0
;
+
∞
.
A.
m
∈
ℝ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = mx + 2 m + 1 x − m nghịch biến trên khoảng 0 ; + ∞ .
A. m ∈ ℝ \ − 1
B. m ∈ − ∞ ; 0 \ − 1
C. m ∈ 0 ; + ∞
D. m ∈ ℝ
Tìm tất cả các giá trị của tham số m để hàm số
y
2
cos
s
x
+
3
2
c
o
s
x
-
m
nghịch biến trên khoảng
0
;
π
3...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = 2 cos s x + 3 2 c o s x - m nghịch biến trên khoảng 0 ; π 3
![]()
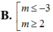
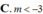
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số
y
2
+
m
x
2
x
+
m
nghịch biến trên từng khoảng xác định của nó A.
m
≤
-
2
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = 2 + m x 2 x + m nghịch biến trên từng khoảng xác định của nó
A. m ≤ - 2 m ≥ 2
B. - 2 < m < 2
C. - 2 ≤ m ≤ 2
D. m < - 2 m > 2