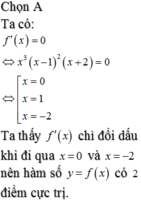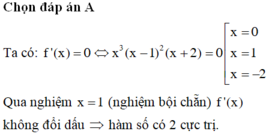Những câu hỏi liên quan
Câu 5. Cho hàm số f x có đạo hàm liên tục tên R và có đạo hàm ' 2 f x x x 9 1 .Tìm m để hàm số 2 y f x x m 2 đồng biến trên 1,3
Cho các mệnh đề :1) Hàm số yf(x) có đạo hàm tại điểm
x
0
thì nó liến tục tại
x
0
. 2) Hàm số yf(x) liên tục tại
x
0
thì nó có đạo hàm tại điểm
x
0
.3) Hàm số yf(x) liên tục trên đoạn [a;b] và f(a).f(b)0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).4) Hàm số yf(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị n...
Đọc tiếp
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Cho hàm số yf(x) liên tục trên R và có đạo hàm
f
(
x
)
x
3
(
x
+
1
)
2
(
x
-...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đạo hàm f ' ( x ) = x 3 ( x + 1 ) 2 ( x - 2 ) Hàm số y=f(x)có bao nhiêu điểm cực trị?
A. 3
B. 1
C. 0
D. 2
Cho hàm số yf(x) liên tục trên
ℝ
, có đạo hàm
f
(
x
)
x
3
(
x
−
1
)
2
(
x
+
2
)
. Hỏi hàm số
y
f...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ , có đạo hàm f ' ( x ) = x 3 ( x − 1 ) 2 ( x + 2 ) . Hỏi hàm số y = f ( x ) có bao nhiêu điểm cực trị?
A. 3
B. 1
C. 0
D. 2
Đáp án D.
Ta có thể lập bảng xét dấu của f'(x) tuy nhiên thì ta có thể dùng mẹo như sau. Tại x=0; x=-2 thì y' đổi dấu do có mũ la lẻ còn x=1 thì không đổi dấu do mũ là chẵn. Vì vậy ta có thể có 2 cực trị.
Đúng 0
Bình luận (0)
Cho hàm số y = f ( x ) liên tục trên R, có đạo hàm f ' ( x ) = x 3 ( x - 1 ) 2 ( x + 2 ) . Hỏi hàm số y = f ( x ) có bao nhiêu điểm cực trị
A. 2
B. 0
C. 1
D. 3
Cho hàm số yf(x) liên tục trên R, có đạo hàm f(x)
x
(
x
-
1
)
2
(
x
+
1
)
2
. Hàm số đã cho có bao nhiêu điểm cực trị A. Có đúng 3 điểm cực trị B. Không có điểm cực trị C. Có đúng 1 điểm cực trị D. Có đúng 2 điểm cực trị
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R, có đạo hàm f'(x)= x ( x - 1 ) 2 ( x + 1 ) 2 . Hàm số đã cho có bao nhiêu điểm cực trị
A. Có đúng 3 điểm cực trị
B. Không có điểm cực trị
C. Có đúng 1 điểm cực trị
D. Có đúng 2 điểm cực trị
Cho hàm số
y
f
(
x
)
liên tục trên R và có đạo hàm
f
(
x
)
(
1
-
x
)
2
(
x
+
1
)
3
(
3
-
x
)
. Hàm số
y
f
(
x
)
đồng biến trên khoảng nào dưới đây
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = ( 1 - x ) 2 ( x + 1 ) 3 ( 3 - x ) . Hàm số y = f ( x ) đồng biến trên khoảng nào dưới đây
![]()
![]()
![]()
![]()
Cho hàm số
y
f
(
x
)
liên tục trên R, có đạo hàm
f
(
x
)
x
3
(
x
−
1
)
2
(
x
+
2
)
.
Hỏi hàm số có bao nhiêu điểm cực trị? A. 2 B. 0 C. 1 D. 3
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R, có đạo hàm f ' ( x ) = x 3 ( x − 1 ) 2 ( x + 2 ) . Hỏi hàm số có bao nhiêu điểm cực trị?
A. 2
B. 0
C. 1
D. 3
Cho hàm số yf(x) liên tục trên R, có đạo hàm
f
’
(
x
)
x
(
x
–
1
)
2
(
x
+
1
)
3
. Đồ...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R, có đạo hàm f ’ ( x ) = x ( x – 1 ) 2 ( x + 1 ) 3 . Đồ thị hàm số y=f(x) có bao nhiêu điểm cực trị?
A. Đồ thị hàm số f(x) không có điểm cực trị
B. Đồ thị hàm số f(x) có 1 điểm cực trị
C. Đồ thị hàm số f(x) có 2 điểm cực trị
D. Đồ thị hàm số f(x) có 3 điểm cực trị
Câu 23: Cho hàm số y f(x) có đạo hàm liên tục trên R và có đồ thị như hình vẽ bên. Hàm số y f(3 - 2x) tăng trên khoảng nào:Hình 3: Đồ thị yf(x)
Đọc tiếp
Câu 23: Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị như hình vẽ bên. Hàm số y = f(3 - 2x) tăng trên khoảng nào:

Hình 3: Đồ thị y=f(x)