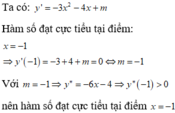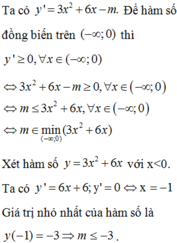y = | x3 + 2x2 -mx + m-1 |. Xđ m để max trên [0;2] = 20

Những câu hỏi liên quan
Tìm m để hàm số
y
x
3
+
2
x
2
-
m
x
+
1
đồng biến trên R. A.
m
-
4
3
B.
m
≤
-
4
3
C.
m
≥
-
4
3
D.
m
-...
Đọc tiếp
Tìm m để hàm số y = x 3 + 2 x 2 - m x + 1 đồng biến trên R.
A. m < - 4 3
B. m ≤ - 4 3
C. m ≥ - 4 3
D. m > - 4 3
Cho hàm số
f
x
x
3
-
2
x
2
-
m
x
-
2018
. Tìm m để
f
x
0
∀
x
∈
0
;
2
A. m 4 B. m 4 C.
m
≤
4
D.
m
≥
4
Đọc tiếp
Cho hàm số f x = x 3 - 2 x 2 - m x - 2018 . Tìm m để f ' x < 0 ∀ x ∈ 0 ; 2
A. m < 4
B. m > 4
C. m ≤ 4
D. m ≥ 4
Ta có f ' x < 0 ∀ x ∈ 0 ; 2 ⇔ 3 x 2 - 4 x - m < 0 ⇔ m > 3 x 2 - 4 x
Xét hàm số g x = 3 x 2 - 4 x trên khoảng ( 0;2 )
Lập bảng biến thiên, ta suy ra m ≥ 4
Đáp án D
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hàm số
y
x
3
-
2
x
2
+
m
x
+
1
đạt cực đại tại x 1. A.m -1 B. m 1 C. m 4/3 D. Không tồn tại.
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = x 3 - 2 x 2 + m x + 1 đạt cực đại tại x = 1.
A.m = -1
B. m = 1
C. m = 4/3
D. Không tồn tại.
Ta có y ' = 3 x 2 - 4 x + m
Hàm số đạt cực trị tại x = 1 thì y'(1) = 0 ⇒ 3 . 1 2 - 4 . 1 + m = 0 ⇒ m = 1
Với m = 1 thì hàm số đã cho trở thành y = x 3 - 2 x 2 + x + 1
Ta có y ' = 3 x 2 - 4 x + 1 , y'' = 6x - 4 Vì y''(1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1.
Do vậy không có m thỏa mãn. Chọn đáp án D.
Chú ý. Sai lầm có thể gặp phải: khi giải y'(1) = 0 => m = 1 đã vội kết luận mà không kiểm tra lại, dẫn đến chọn đáp án B.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hàm số y -x3 + 2x2 + mx đạt cực đại tại x 1 A. m -1 B. m -1 C. m ≠ -1 D. m -1
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = -x3 + 2x2 + mx đạt cực đại tại x = 1
A. m = -1
B. m > -1
C. m ≠ -1
D. m < -1
Đáp án A.
Ta có: y’ = -3x2 + 4x + m.
y’’ = -6x + 4.
+ y’(1) = 0 <=> -3 + 4 + m = 0 ó m = -1.
+ y’’(1) = -2 < 0 thỏa
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số thực m để hàm số
y
−
x
3
−
2
x
2
+
m
x
+
1
đạt cực tiểu tại điểm x -1 A. m -1 B.
m
≠
−
1
C. m -1 D. m -1
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để hàm số y = − x 3 − 2 x 2 + m x + 1 đạt cực tiểu tại điểm x = -1
A. m < -1
B. m ≠ − 1
C. m = -1
D. m > -1
Tìm tất cả các giá trị của tham số thực m để hàm số y = - x 3 - 2 x 2 + m x + 1 đạt cực tiểu tại điểm x = -1
A. m < -1
B. m ≠ -1
C. m = -1
D. m > -1
Đáp án C
Phương pháp:
Hàm số bậc ba y = f(x) đạt cực tiểu tại x = x0 khi và chỉ khi
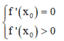
Cách giải:
![]()
![]()
![]()
![]()
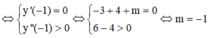
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hàm số
y
x
2
+
2
x
2
-
m
x
+
1
đồng biến trên khoảng (-∞;0) A. m ≥ -2 B. m ≤ -3 C.m ≤ -1 D.m ≤ 0
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = x 2 + 2 x 2 - m x + 1 đồng biến trên khoảng (-∞;0)
A. m ≥ -2
B. m ≤ -3
C.m ≤ -1
D.m ≤ 0
Cho đồ thị
C
m
:
y
x
3
-
2
x
2
+
1
-
m
x
+
m
. Tất cả giá trị của tham số m để
C
m
cắt trục hoành tại ba điểm phân biệt có hoành độ
x...
Đọc tiếp
Cho đồ thị C m : y = x 3 - 2 x 2 + 1 - m x + m . Tất cả giá trị của tham số m để C m cắt trục hoành tại ba điểm phân biệt có hoành độ x 1 , x 2 , x 3 thỏa mãn x 1 2 + x 2 2 + x 3 2 = 4 là
A. m = 1
B. m ≠ 0
C. m = 2
D. m > - 1 4 v à m ≠ 0
Tìm các giá trị của tham số m để hàm số
y
x
3
+
3
x
2
+
m
x
+
m
: có
y
≤
0
trên một đoạn có độ dài bằng 1. A.
m
9
4
B.
m
4
9
C.
m
2
D.
m
1...
Đọc tiếp
Tìm các giá trị của tham số m để hàm số y = x 3 + 3 x 2 + m x + m : có y ' ≤ 0 trên một đoạn có độ dài bằng 1.
A. m = 9 4
B. m = 4 9
C. m = 2
D. m = 1 2