Hàm số y = 1 3 x 3 − 2 x 2 + 3 x − 1 nghịch biến trên khoảng nào trong các khoảng sau đây?
A. − 1 ; 3
B. 1 ; 4
C. − 3 ; − 1
D. 1 ; 3
Đáp án D
Tập xác định D = ℝ
y ' = x 2 − 4 x + 3 < 0 ⇔ 1 < x < 3.
Do đó hàm số nghịch biến trên khoảng 1 ; 3
Hàm số y = 1 3 x 3 − 2 x 2 + 3 x − 1 nghịch biến trên khoảng nào trong các khoảng sau đây?
A. (1;4)
B. (1;3)
C. (-3;-1)
D. (-1;3)
Đáp án B
Ta có y ' = x 2 − 4 x + 3 = x − 1 x − 3 ⇒ y ' < 0 ⇔ 1 < x < 3
Suy ra hàm số nghịch biến trên khoảng (1;3)
Khoảng nghịch biến của hàm số y= 1/2x^4-3x^2-3 là gì các bạn?
Hàm số y= x^2/1-x đồng biến trên khoảng nào?
Hàm số y= x^3+3x^2 nghịch biến trên khoảng nào?
Khoảng nghịch biến của hàm số y y = x 3 3 - 2 x 2 + 3 x + 5 là:
A. (1;3)
B.(-∞; 1) ∪ (3; +∞)
C. (-∞; 1) và (3; +∞)
D. (1;+∞)
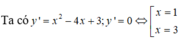
Bảng xét dấu y’ :
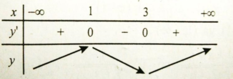
Vậy hàm số nghịch biến trên khoảng (1;3).
Chọn đáp án A.
Vẽ đồ thị của các hàm số \(y=3x+1\) và \(y=-2x^2\). Hãy cho biết:
a) Hàm số \(y=3x+1\) đồng biến hay nghịch biến trên R.
b) Hàm số \(y=-2x^2\) đồng biến hay nghịch biến trên mỗi khoảng: \(\left(-\infty;0\right)\) và \(\left(0;+\infty\right)\)
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)
a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Khẳng định nào sau đây đúng?
A. y = sin3x là hàm số chẵn
B. Hàm số y = 3 x + 5 x - 1 xác định trên R
C. Hàm số y = x 3 + 4x - 5 đồng biến trên R
D. Hàm số y = sinx + 3x - 1 nghịch biến trên R
Đáp án: C.
Vì y' = 3 x 2 + 4 > 0, ∀ x ∈ R.
Hàm số y = x 3 − 3 x + 1 nghịch biến trên khoảng
A. (0;2)
B. 1 ; + ∞
C. − ∞ ; − 1
D. - 1 ; 1
Cho hàm số y = x 4 - 2 x 2 + 1 . Xét các mệnh đề sau đây
1) Hàm số có 3 điểm cực trị;
2) Hàm số đồng biến trên các khoảng - 1 ; 0 ; 1 ; + ∞
3) Hàm số có 1 điểm cực trị;
4) Hàm số nghịch biến trên các khoảng - ∞ ; - 1 ; 0 ; 1
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên?
A. 2
B. 1
C. 4
D. 3
Hàm số y = x 2 + 3 x + 1 nghịch biến trên khoảng nào?
A. (-3;1).
B. (1; +∞).
C. (-∞; -3).
D. (-3; -1) và (-1; 1)
Đáp án D
Ta có: D = R và
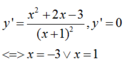
Vậy hàm số nghịch biến trên các khoảng (-3; -1) và (-1; 1)
Hàm số y = 2 x + 3 x - 1 nghịch biến trên các khoảng:
A. R \ {1}
B. (-∞; 1) và (1; +∞)
C. (-∞; 2) và (2; +∞)
D. (-∞; -5) và (-5; +∞)
