Trên hệ tọa độ Oxy,cho A(-1;3);B(2;4);C(0;1) .Tìm điểm E thuộc đường thẳng d:y=x+1 sao cho ABEC là hình thang

Những câu hỏi liên quan
1. Trg mp hệ tọa độ Oxy , cho A(-1;0),B(3;-2) . Đỉnh C của tam giác ABC vuông tại A nằm trên đt nào ?2. Cho các số thực x,y thỏa mãn 0 x,yle1 và x+y 4xy . Tìm GTLN của biểu thức Mx^2+y^2-7xy3. Trên hệ trục tọa độ Oxy cho tam giác ABC . Biết B (3;-2),C(-1;1) và AB2AC. Tìm tọa độ D là chân đg phân giác trg của tam giác ABCHelp me !
Đọc tiếp
1. Trg mp hệ tọa độ Oxy , cho A(-1;0),B(3;-2) . Đỉnh C của tam giác ABC vuông tại A nằm trên đt nào ?
2. Cho các số thực x,y thỏa mãn \(0< x,y\le1\) và x+y= 4xy . Tìm GTLN của biểu thức \(M=x^2+y^2-7xy\)
3. Trên hệ trục tọa độ Oxy cho tam giác ABC . Biết B (3;-2),C(-1;1) và AB=2AC. Tìm tọa độ D là chân đg phân giác trg của tam giác ABC
Help me !
Trong mp với hệ tọa đô Oxy cho hai điểm A(1;-2), B(-4;5). Tìm tọa độ điểm M trên trục Oy sao cho 3 điểm M,A,B thẳng hàng
Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
Đúng 2
Bình luận (0)
trong hệ tọa độ Oxy , cho 2 điểm A( 2;2 ) và B( 1;5 ) . tìm tọa độ điểm M trên trục tung sao cho độ dài MA + MB nhỏ nhất
Trên hệ trục tọa độ Oxy, cho các điểm A(-3; 1), B(-1; 1), C(-3; 3). Tam giác ABC là tam giác gì?
A. Tam giác đều
B. Tam giác cân
C. Tam giác vuông
D. Tam giác tù
Biểu diễn ba điểm A, B, C trên hệ trục tọa độ Oxy ta được
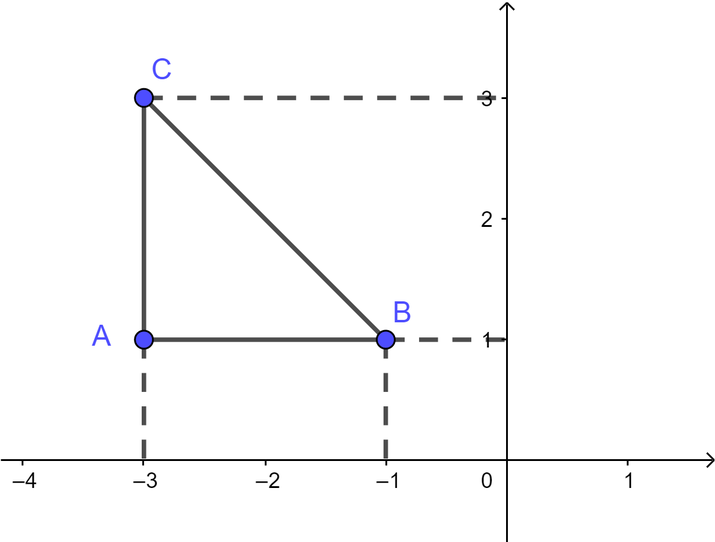
Quan sát hình vẽ ta thấy tam giác ABC là tam giác vuông tại A
Chọn đáp án C
Đúng 0
Bình luận (0)
1. Trong hệ trục tọa độ Oxy có A(2;3) B(1;4), C(-1;-5)
tìm tọa độ điểm I trên AB sao cho \(\left|\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}\right|\) có giá trị nhỏ nhất
\(\overrightarrow{AB}=\left(-1;1\right)\) nên pt AB có dạng:
\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\)
Do I thuộc AB nên tọa độ có dạng: \(I\left(a;5-a\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=\left(2-a;a-2\right)\\\overrightarrow{IB}=\left(1-a;a-1\right)\\\overrightarrow{IC}=\left(-1-a;a-10\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}=\left(-9a;9a-55\right)\)
\(\Rightarrow\left|\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}\right|=\sqrt{\left(9a\right)^2+\left(55-9a\right)^2}\ge\sqrt{\dfrac{1}{2}\left(9a+55-9a\right)^2}=\dfrac{55}{\sqrt{2}}\)
Dấu "=" xảy ra khi \(9a=55-9a\Rightarrow a=\dfrac{55}{18}\Rightarrow I\left(\dfrac{55}{18};\dfrac{35}{18}\right)\)
Kiểm tra lại tính toán
Đúng 2
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho hai điểm A(1; 2), B(3; 4). Tìm hệ số a của đường thẳng đi qua A và B
Đường thẳng đi qua hai điểm A và B có dạng: y = ax + b
Đường thẳng đi qua hai điểm A và B nên tọa độ A và B nghiệm đúng phương trình.
Ta có: Tại A: 2 = a + b ⇔ b = 2 – a (1)
Tại B: 4 = 3a + b (2)
Thay (1) và (2) ta có: 4 = 3a + 2 – a ⇔ 2a = 2 ⇔ a = 1
Vậy hệ số a của đường thẳng đi qua A và B là 1.
Đúng 0
Bình luận (0)
Vẽ một hệ trục tọa độ Oxy với đơn vị trên hai trục bằng nhau và biểu diễn các điểm trên hệ trục tọa độ đó.
Xem chi tiết
A(-3;2); B(4;-1); C(3;2); D(-2;-1)
Trong mặt phẳng tọa độ với hệ tọa độ Oxy, cho hai điểm A(-2,3), B(1,-6). Tọa độ vecto AB là?
\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)
Đúng 0
Bình luận (0)
Trong mặt tọa độ Oxy, cho đường thẳng (d): y 2x + m2 – m + 5 và parabol (P): y x2 . a. Với m 1, vẽ đường thẳng (d) và parabol (P) trên cùng hệ trục tọa độ Oxy. b. Chứng minh đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt với mọi m. c. Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn (x1 + 1)(x2 + 1) –2. d*. Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x...
Đọc tiếp
Trong mặt tọa độ Oxy, cho đường thẳng (d): y = 2x + m2 – m + 5 và parabol (P): y = x2 . a. Với m = 1, vẽ đường thẳng (d) và parabol (P) trên cùng hệ trục tọa độ Oxy. b. Chứng minh đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt với mọi m. c. Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn (x1 + 1)(x2 + 1) = –2. d*. Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn |2x1| – |x2| = 1.
Trên hệ trục tọa độ Oxy với đơn vị trên 2 trục bằng nhau cho các điểm A(1;5), B(3;1), C(-3;-3).
1) vẽ hệ trục tọa độ Oxy và các điểm A, B,C
2) viết phương trình đường thẳng OA
3) tính diện tích tam giác ABC nếu biết đơn vị trên các trục là 1cm.
mọi người giúp mik với, mik đang cần gấp.........












