Cho (S) là mặt cầu tâm I(3;0;0) và tiếp xức với mặt phẳng (P) có phương trình 2x - 2y - z + 3 = 0. Khi đó, bán kính của (S) là
A. 6
B. 4
C. 2
D. 3
Những câu hỏi liên quan
Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là: A.
(
x
-
1
)
2
+
(
y
-
...
Đọc tiếp
Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R=3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là:
A. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 9
B. ( x + 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 9
C. x 2 + y 2 + z 2 - 2x - 4y + 2z - 3 = 0
D. x 2 + y 2 + z 2 = 9
Đáp án B
Mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ nên mặt cầu (S’) có tâm I’(-1;-2; 1) đối xứng với I qua gốc O và có bán kính R’ = R = 3.
Phương trình mặt cầu (S’) là: ( x + 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 9
Đúng 0
Bình luận (0)
Cho mặt cầu (S) có tâm I và bán kính R 3. Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C) có chu vi 2ᴨ. Tính khoảng cách d từ tâm I đến mặt phẳng (P). A.
d
2
B.
d
2
2
C.
d
7
2
D.
d
7
Đọc tiếp
Cho mặt cầu (S) có tâm I và bán kính R = 3. Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C) có chu vi 2ᴨ. Tính khoảng cách d từ tâm I đến mặt phẳng (P).
A. d = 2
B. d = 2 2
C. d = 7 2
D. d = 7
Cho mặt cầu (S) có tâm I(2;1;-1) và tiếp xúc với mặt phẳng (
α
) có phương trình 2x-2y-z +3 0. Bán kính mặt cầu (S) là A.
2
9
B. 2 C.
2
3
D.
4
3
Đọc tiếp
Cho mặt cầu (S) có tâm I(2;1;-1) và tiếp xúc với mặt phẳng ( α ) có phương trình 2x-2y-z +3 = 0. Bán kính mặt cầu (S) là
A. 2 9
B. 2
C. 2 3
D. 4 3
Đáp án B
Ta có: bán kính mặt cầu tâm I tiếp xúc với mặt phẳng ( α ) là khoảng cách từ I đến mặt phẳng
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là: A.
(
x
-
1
)
2
+
(
y
+
2...
Đọc tiếp
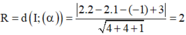
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là:
A. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 3
B. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9
C. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 3
D. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 9
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có tâm I(-1;2;0) và bán kính R3. Phương trình mặt cầu (S) là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có tâm I(-1;2;0) và bán kính R=3. Phương trình mặt cầu (S) là:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có tâm I(-1;2;0) và bán kính R3. Phương trình mặt cầu (S) là: A.
(
x
+
1
)
2
+
(
y
-
2
)
2
+
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có tâm I(-1;2;0) và bán kính R=3. Phương trình mặt cầu (S) là:
A. ( x + 1 ) 2 + ( y - 2 ) 2 + z 2 = 3
B. ( x + 1 ) 2 + ( y - 2 ) 2 + z 2 = 9
C. ( x - 1 ) 2 + ( y + 2 ) 2 + z 2 = 9
D. ( x + 1 ) 2 + ( y - 2 ) 2 + z 2 = 3
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
+
2
x
−
4
y
−
2
z
−
3
0
. Tọa độ tâm I của mặt cầu (S) là A. (-1;2;1) B. (2;-4;-2) C. (1;-2;-1) D. (-2;4;2)
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 + 2 x − 4 y − 2 z − 3 = 0 . Tọa độ tâm I của mặt cầu (S) là
A. (-1;2;1)
B. (2;-4;-2)
C. (1;-2;-1)
D. (-2;4;2)
Trong không gian Oxyz, cho hai mặt cầu (S) và (S’) có tâm lần lượt là I(-1;2;3), I’(3;-2;1) và có bán kính lần lượt là 4 và 2. Cho điểm M di động trên mặt cầu (S), N di động trên mặt cầu (S’). Khi đó giá trị lớn nhất của đoạn thẳng MN bằng: A. 8 B. 2 C. 12 D. 6
Đọc tiếp
Trong không gian Oxyz, cho hai mặt cầu (S) và (S’) có tâm lần lượt là I(-1;2;3), I’(3;-2;1) và có bán kính lần lượt là 4 và 2. Cho điểm M di động trên mặt cầu (S), N di động trên mặt cầu (S’). Khi đó giá trị lớn nhất của đoạn thẳng MN bằng:
A. 8
B. 2
C. 12
D. 6
Đáp án C
Ta có: II' = 6 = R + R'
Ta có: MN ≥ MI + II' + I'N = R + 6 + R' = 12
Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.
Đúng 0
Bình luận (0)
Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I (0; -2; 1) và mặt phẳng (P): x + 2y - 2z + 3 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích là 2π. Viết phương trình mặt cầu (S). A.
(
S
)
:
x
2
+
(
y
+...
Đọc tiếp
Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I (0; -2; 1) và mặt phẳng (P): x + 2y - 2z + 3 = 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích là 2π. Viết phương trình mặt cầu (S).
A. ( S ) : x 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 3
B. ( S ) : x 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 1
C . ( S ) : x 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 3
D. ( S ) : x 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 2
Chọn C
Ta có h = d(I, (P)) = 1
Gọi (C) là đường tròn giao tuyến có bán kính r.
Vì S = r2.π = 2π <=> r = √2
Mà R2 = r2 + h2 = 3 => R = √3
Vậy phương trình mặt cầu tâm i (0; -2; 1) và bán kính R = √3
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
3
x
2
+
3
y
2
+
3
z
2
+ 6x - 8y + 15z - 3 0Tìm tọa độ tâm I và bán kính R của mặt cầu (S). A.
I
-
1
;
4
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
3 x 2 + 3 y 2 + 3 z 2 + 6x - 8y + 15z - 3 = 0
Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
A. I - 1 ; 4 3 ; - 5 2 , R = 361 36
B. I - 1 ; 4 3 ; - 5 2 , R = 19 6
C. I - 3 ; 4 ; - 15 2 , R = 19 6
D. I 3 ; - 4 ; 15 2 , R = 361 36
