Tìm bán kính của đường tròn tâm \(C\left(-2;-2\right)\), tiếp xúc với đường thẳng \(\Delta:5x+12y-10=0\)

Những câu hỏi liên quan
Tìm tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} = 7\).
Phương trình của \(\left( C \right)\) là \({\left( {x - \left( { - 2} \right)} \right)^2} + {\left( {y - 4} \right)^2} = {\left( {\sqrt 7 } \right)^2}\).
Vậy \(\left( C \right)\) có tâm \(I\left( { - 2;4} \right)\) và bán kính \(R = \sqrt 7 \).
Đúng 0
Bình luận (0)
Tìm tâm và bán kính của đường tròn \({\left( {x + 3} \right)^2} + {\left( {y - 3} \right)^2} = 36\)
Phương trình của \(\left( C \right)\) là: \({\left( {x - \left( { - 3} \right)} \right)^2} + {\left( {y - 3} \right)^2} = {6^2}\). Vậy \(\left( C \right)\) có tâm \(I\left( { - 3;3} \right)\) và \(R = 6\).
Đúng 0
Bình luận (0)
Cho hình tròn tâm a bán kính 2 cm hình tròn tâm b bán kính 4 cm .ghi đúng hoặc sai vào các đâp an.A:Đường kính của hình tròn tâm a có độ dài là 4 cm B: đường kính hình tròn tâm b có bán kính là 2cm C: đường kính của hình tròn tâm a dai mgaaps đôi đường kính hình tròn tâm b.D: đường kính của hình tròn tâm b dài gấp 4 lần đường kính của hình tròn tâm a
Bán kính hình tròn đó là:
6:2=3( cm )
Đáp số:3 cm
Đúng 0
Bình luận (0)
Vẽ hình liên tiếp theo các cách diễn đạt sau :
a) Vẽ đoạn thẳng AB 2cm. Vẽ đường tròn (C_1) tâm A, bán kính AB
b) Vẽ đường tròn left(C_2right) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn left(C_1right) là C và G
c) Vẽ đường tròn left(C_3right) tâm C, bán kính AC. Gọi các giao điểm mới của đường tròn này với đường tròn left(C_1right) là D
d) Vẽ đường tròn left(C_4right) tâm D, bán kính AD. Gọi các giao điểm mới của đường tròn này với đường tròn left(C_1right) là...
Đọc tiếp
Vẽ hình liên tiếp theo các cách diễn đạt sau :
a) Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (\(C_1\)) tâm A, bán kính AB
b) Vẽ đường tròn \(\left(C_2\right)\) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn \(\left(C_1\right)\) là C và G
c) Vẽ đường tròn \(\left(C_3\right)\) tâm C, bán kính AC. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là D
d) Vẽ đường tròn \(\left(C_4\right)\) tâm D, bán kính AD. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là E
e) Vẽ đường tròn \(\left(C_5\right)\) tâm E, bán kính AE. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là F
f) Vẽ đường tròn \(\left(C_6\right)\) tâm F, bán kính AF.
g) Vẽ đường tròn \(\left(C_7\right)\) tâm G, bán kính AG
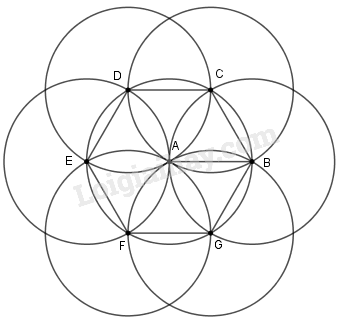
Sau khi vẽ như trên, hãy so sánh các đoạn thẳng AB, BC, CD, DE, EF, FG, GB
Vẽ hình liên tiếp theo các cách diễn đạt sau:a. Vẽ đoạn thẳng AB2cm. Vẽ đường tròn (C1) tâm A , bán kính ABb. Vẽ đường tròn (C2) tâm B bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (C1) là C và G.c. Vẽ đường tròn (C3) tâm C, bán kính AC. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là Dd. Vẽ đường tròn (C4) tâm D bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là Ee. Vẽ đường tròn (C5) tâm E bán kính AE. Gọi giao điểm mới của đường tròn này...
Đọc tiếp
Vẽ hình liên tiếp theo các cách diễn đạt sau:
a. Vẽ đoạn thẳng AB=2cm. Vẽ đường tròn (C1) tâm A , bán kính AB
b. Vẽ đường tròn (C2) tâm B bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (C1) là C và G.
c. Vẽ đường tròn (C3) tâm C, bán kính AC. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là D
d. Vẽ đường tròn (C4) tâm D bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là E
e. Vẽ đường tròn (C5) tâm E bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là F
f. Vẽ đường tròn (C6) tâm F bán kính AF
g. Vẽ đường tròn (C7) tâm G bán kính AG
Sau khi vẽ như trên hãy so sánh các đoạn thẳng AB, BC, CD, DE, EF, FG, GB
Sau khi vẽ ta được hình như sau:
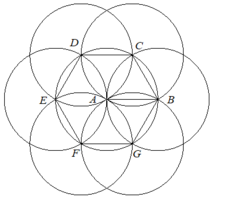
Khi đó, các đoạn thẳng A B = B C = C D = D E = E F = F G = G B (vì cùng bằng bán kính).
Đúng 0
Bình luận (0)
Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó
a) \({x^2} + {y^2} - 2x - 4y - 20 = 0\)
b) \({\left( {x + 5} \right)^2} + {\left( {y + 1} \right)^2} = 121\)
c) \({x^2} + {y^2} - 4x - 8y + 5 = 0\)
d) \(2{x^2} + 2{y^2} + 6x + 8y - 2 = 0\)
a) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 1,b = 2,c = - 20\)
Ta có \({a^2} + {b^2} - c = 1 + 4 + 20 = 25 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(1;2)\) và có bán kính \(R = \sqrt {25} = 5\)
b) Phương trình \({\left( {x + 5} \right)^2} + {\left( {y + 1} \right)^2} = 121\) là phương trình dường tròn với tâm \(I( - 5; - 1)\) và bán kinh \(R = \sqrt {121} = 11\)
c) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = - 3,b = - 2,c = - 2\)
Ta có \({a^2} + {b^2} - c = 9 + 4 + 2 = 15 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I( - 3; - 2)\) và có bán kính \(R = \sqrt {15} \)
d) Phương trình không có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) nên phương trình đã cho không là phương trình đường tròn
Đúng 0
Bình luận (0)
Vẽ hình liên tiếp theo cách diễn đạt sauVẽ đoạn thẳng AB 2cm. Vẽ đường tròn (c1) tâm A, bán kính AB.Vẽ đường tròn (c2) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (c1) là C và G.Vẽ đường tròn (c3) tâm C, bán kính AC. Goi giao điểm mới củađường tròn này với đường tròn (c1) là D.Vẽ đường tròn (c4) tâm D, bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là E.Vẽ đường tròn (c5) tâm E, bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (...
Đọc tiếp
Vẽ hình liên tiếp theo cách diễn đạt sau
Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (c1) tâm A, bán kính AB.
Vẽ đường tròn (c2) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (c1) là C và G.
Vẽ đường tròn (c3) tâm C, bán kính AC. Goi giao điểm mới củađường tròn này với đường tròn (c1) là D.
Vẽ đường tròn (c4) tâm D, bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là E.
Vẽ đường tròn (c5) tâm E, bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là F
Vẽ đường tròn (c6) tâm F, bán kính AF.
Vẽ đường tròn (c7) tâm G, bán kính AG.
Sau khi vẽ như trên hãy so sánh các đoạn thẳng: AB, BC, CD, DE, EF, FG, GB
Sau khi vẽ ta được hình bs.17
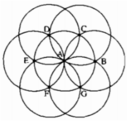
Khi đó, các đoạn thẳng: AB, BC, CD, EF, FG, GB bằng nhau (vì cùng bằng bán kính).
Đúng 0
Bình luận (0)
Tìm tâm và bán kính của các đường tròn có phương trình:
a) \({\left( {x - 2} \right)^2} + {\left( {y - 7} \right)^2} = 64\)
b) \({\left( {x + 3} \right)^2} + {\left( {y + 2} \right)^2} = 8\)
c) \({x^2} + {y^2} - 4x - 6y - 12 = 0\)
a) Phương trình đường tròn \({\left( {x - 2} \right)^2} + {\left( {y - 7} \right)^2} = 64\) có dạng \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) nên đường tròn có tâm là \(I(2;7)\) và bán kinh \(R = \sqrt {64} = 8\)
b) Phương trình đường tròn \({\left( {x + 3} \right)^2} + {\left( {y + 2} \right)^2} = 8\) có dạng \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) nên đường tròn có tâm là \(I( - 3; - 2)\) và bán kinh \(R = \sqrt 8 = 2\sqrt 2 \)
c) Phương trình đường tròn \({x^2} + {y^2} - 4x - 6y - 12 = 0\) có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) nên đường tròn có tâm là \(I(2;3)\) và bán kinh \(R = \sqrt {{2^2} + {3^2} + 12} = 5\)
Đúng 0
Bình luận (0)
Viết phương trình đường tròn (C) trong các trường hợp sau:
a) (C) có tâm \(O\left( {0;0} \right)\), bán kính \(R = 4\)
b) (C) có tâm \(I\left( {2; - 2} \right)\), bán kính \(R = 8\)
c) (C) đi qua 3 điểm \(A(1;4),B(0;1),C(4;3)\)
a) Đường tròn (C) tâm \(O\left( {0;0} \right)\), bán kính \(R = 4\) có phương trình là: \({x^2} + {y^2} = 16\)
b) Đường tròn (C) tâm \(I\left( {2; - 2} \right)\), bán kính \(R = 8\) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y + 2} \right)^2} = 64\)
c) Gọi M, N lần lượt là trung điểm của AB, AC ta có: \(M\left( {\frac{1}{2};\frac{5}{2}} \right),N\left( {\frac{5}{2};\frac{7}{2}} \right)\)
Đường trung trực \(\Delta \)của đoạn thẳng AB là đường thẳng đi qua M và nhận vt \(\overrightarrow {BA} = (1;3)\) làm vt pháp tuyến, nên có phương trình \(x + 3y - 8 = 0\)
Đường trung trực d của đoạn thẳng AC là đường thẳng đi qua N và nhận vt \(\overrightarrow {AC} = (3; - 1)\) làm vt pháp tuyến, nên có phương trình \(3x - y - 4 = 0\)
\(\Delta \) cắt d tại điểm \(I(2;2)\) cách đều ba điểm A, B, C suy ra đường tròn (C) cần tìm có tâm \(I(2;2)\) và có bán kính \(R = IA = \sqrt 5 \). Vậy (C) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 5\)
Đúng 0
Bình luận (0)