3: cho hàm số f(x)=ax^2+bx+c có tọa độ đỉnh (2;-1) và có giá trị nhỏ nhất khi là -1 khi x=2
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x-2018)-2|=m có đúng 3 nghiệm.
3: cho hàm số f(x)=ax^2+bx+c có tọa độ đỉnh (2;-1) và có giá trị nhỏ nhất khi là -1 khi x=2
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x-2018)-2|=m có đúng 3 nghiệm.
B1: Cho hàm số \(y=f\left(x\right)=x^2+ax-a+5\).Tìm a biết f(-2)=2004
B2: Cho hàm số \(y=f\left(x\right)=ax+b.\)Tìm và b biết f(1)=2 và f(2)=3
B3: Cho hàm số \(y=f\left(x\right)=ax^2+bx+c.\)Tìm a,b,c biết f(o)=1,f(1)=2,f(2)=3
B4:Cho hàm số y=x+1
a,tìm tọa độ điểm A, biết A là giao điểm đồ thị với trục tung
b, Tìm tọa độ điểm B biết B là giao điểm của đồ thị với trục hoành
B5: tìm tọa độ giao điểm của đồ thị hàm số y=2x và y=3x-1
B6: Cho hàm số y=ax^2+bx+c tìm a,b,c biết đồ thị hàm số đi qua điểm A(0,1), B(1,2), C(-1,0)
HELP ME!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
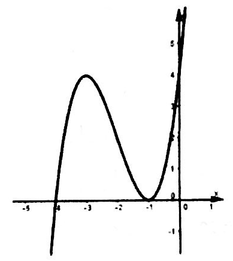
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
cho hàm số : y = f(x) = ax2 + bx + c (P)
tìm a , b , c để đồ thị (P) đi qua A(-1;4) và có đỉnh S(-2;-1)
Ta có : A( -1 ; 4 ) \(\in\)(P) nên 4 = a - b + c (1)
S( -2 ; -1 ) \(\in\)(P) nên -1 = 4a - 2b + c (2)
(P) có đỉnh S( -2 ; -1 ) nên \(X_S=\frac{-b}{2a}\Leftrightarrow4a-b=0\)(3)
Từ (1) , (2) và (3) ta có HPT
\(\hept{\begin{cases}a-b+c=4\\4a-2b+c=-1\\4a-b=0\end{cases}\Leftrightarrow}\hept{\begin{cases}a=5\\b=20\\c=19\end{cases}}\)
Vậy : \(y=f\left(x\right)=5x^2+20x+19\left(P\right)\)
Cho hàm số y = ax2 + bx + c có đồ thị (P). Tọa độ đỉnh của (P) là:
A. 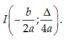
B. 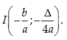
C. 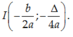
D. 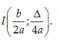
cho hàm số y=ax^2+bx+1. Xác định hàm số biết rằng đồ thị của hàm số đó là parabol có đỉnh I(2;-3)
cho hàm số y=f(x)=ax^2+bx+c.Tim a,b,c biết f(-2)=0;f(2)=0 và a-c=3
Ta có: \(y=f\left(x\right)=ax^{2\:}+bx+c\)
\(\Rightarrow f\left(-2\right)=4a-2b+c=2a-2b+2a+c=2a-2b+3c+6=0\)
\(\Rightarrow2a-2b+3c=-6\left(1\right)\)
\(f\left(2\right)=4a+2b+c=2a+2b+2a+c=2a+2b+3c+6=0\)
\(\Rightarrow2a+2b+3c=-6\left(2\right)\)
Từ (1)(2) \(\Rightarrow2a-2b+3c=2a+2b+3c\)
\(\Rightarrow2a-2b+3c-\left(2a+2b+3c\right)=0\)
\(\Rightarrow2a-2b+3c-2a-2b-3c=0\)
\(\Rightarrow\left(2a-2a\right)-\left(2b+2b\right)+\left(3c-3c\right)=0\)
\(\Rightarrow-4b=0\)
\(\Rightarrow b=0\)
\(\Rightarrow2a+3c=-6\)
\(\Rightarrow5c+6=-6\)
\(\Rightarrow5c=-12\)
\(\Rightarrow c=\frac{-12}{5}\)
\(\Rightarrow a=\frac{-12}{5}+3=\frac{3}{5}\)
Vậy \(a=\frac{3}{5};c=\frac{-12}{5};b=0\)
a) Cho hàm số y=f(x)=ax5+bx3+cx-5 (a,b,c thuộc R)
Cho f(-3)=208. Tính f(3)=?
b) Cho hàm số y=g(x)=ax4-bx2+x+3 (a,b thuộc R)
Cho g(2)=17. Tính g(-2)=?
Cho hàm số y= f(x)= ax^2+bx+c
Tìm a,b,c nếu biết f(0)=2; f(2)=3; f(3)=4.