Trên cùng một hệ trục tọa độ, vẽ đồ thị các hàm số sau: y=2x; y=-2x; y=\(\dfrac{1}{2}x\)
Những câu hỏi liên quan
vẽ trên cùng một hệ trục tọa độ oxy đồ thị của các hàm số
\(y=-2x\)
trên cùng 1 hệ trục tọa độ , vẽ đồ thị các hàm số sau : y=2x , y= âm 2x , y=1/2x
Vẽ đồ thị các hàm số sau trên cùng một hệ trục tọa độ:
a) y = 2x
b) y = -2x
Lời giải:
Đồ thị màu xanh lá: $y=2x$
Đồ thị màu xanh biển: $y=-2x$
Đúng 0
Bình luận (0)
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau: y = 1 2 x
Với x = 1 ta được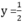 
. Điểm B(1 ; 1/2) thuộc đồ thị của hàm số 
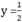x
Vậy đường thằng OB là đồ thị hàm số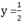 
x
Đúng 0
Bình luận (0)
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau: y = - x
Vẽ hệ trục tọa độ Oxy
Với x = 1 ta được y = -1. Điểm A(1 ;-1) thuộc đồ thị của hàm số y = -x
Vậy đường thằng OA là đồ thị hàm số y = -x
Đúng 0
Bình luận (0)
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau: y = - 1 2 x
Với x = 1 ta được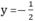 
. Điểm C(1 ; -1/2) thuộc đồ thị của hàm số 
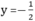x
Vậy đường thằng OC là đồ thị hàm số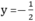 
x
Vẽ đồ thị:
Đúng 0
Bình luận (0)
Vẽ trên cùng một hệ trục tọa độ, đồ thì các hàm số y=x và y=2x-2. Tìm tọa độ giao điểm A của hai đồ thị trên (bằng phép tính)
Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x. Vẽ đường thẳng qua B(0; 2) và E(-1; 0) được đồ thị hàm số y = 2x - 2.
Đúng 0
Bình luận (0)
Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau đây:
y = x ( d 1 )
y = 2x ( d 2 )
y = -x + 3 ( d 3 )
*Vẽ đồ thị của hàm số y = x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 1
Đồ thị hàm số y = x là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm (1; 1)
*Vẽ đồ thị hàm số y = 2x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 2
Đồ thị hàm số y = 2x là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm (1;2)
*Vẽ đồ thị của hàm số y = -x + 3
Cho x = 0 thì y = 3. Ta có điểm (0; 3)
Cho y = 0 thì x = 3. Ta có điểm (3; 0)
Đồ thị hàm số y = -x + 3 là đường thẳng đi qua hai điểm (0; 3) và (3; 0)
Đúng 0
Bình luận (0)
hãy vẽ đồ thị hàm hàm số sau trên cùng hệ trục tọa độ đó y=3x y=-1/2 y=-2x
Vẽ đồ thị của các hàm số sau trên cùng một hệ trục tọa độ:
y = |x|;
y = |x + 1|.
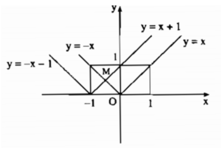
Ta vẽ đồ thị y = x với x ≥ 0.
Vẽ đồ thị y = -x với x ≤ 0.
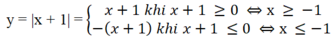
Ta vẽ đồ thị y = x + 1 với x ≥ -1
Vẽ đồ thị y = -x – 1 với x ≤ -1.
Đúng 0
Bình luận (0)