Giả sử x và y là hai đại lượng tỉ lệ thuận x1 ,x2 là hai giá trị khác nhau của x và y1; y2là hai gía trị của y .Tìm x1,y1biết
3y1+ 2x1= 24 , x2= -5, y2= 3
Những câu hỏi liên quan
giả sử x và y là hai đại lượng tỉ lệ thuận x1 x2 là hai giá trị khác nhau của x và y hai giá trị của y.Tìm x1;y1 biết y1-3x1=-7,x2=-4,y2=3
Giả sử x và y là hai đại lượng tỉ lệ thuận
x
1
,
x
2
là hai giá trị khác nhau của x và
y
1
,
y
2
là hai gía trị của y . Tìm
x
1
,
...
Đọc tiếp
Giả sử x và y là hai đại lượng tỉ lệ thuận x 1 , x 2 là hai giá trị khác nhau của x và y 1 , y 2 là hai gía trị của y . Tìm x 1 , y 1 biết: y 1 -3 x 1 = -7 , x 2 = -4 , y 2 = 3
A. x 1 = − 28 ; y 1 = 21
B. x 1 = − 3 ; y 1 = 4
C. x 1 = − 4 ; y 1 = 3
D. x 1 = 4 ; y 1 = − 3
Suy ra x 1 − 4 = y 1 3 = y 1 − x 1 3 − ( − 4 ) = − 7 7 = − 1
Nên x 1 = ( − 1 ) . ( − 4 ) = 4 ; y 1 = ( − 1 ) .3 = − 3
Đáp án cần chọn là D
Đúng 0
Bình luận (0)
Giả sử x và y là hai đại lượng tỉ lệ thuận;
x
1
,
x
2
là hai giá trị khác nhau của x và
y
1
,
y
2
là hai giá trị tương ứng của y. Tính
x
1
biết
x
2
3
,
y...
Đọc tiếp
Giả sử x và y là hai đại lượng tỉ lệ thuận; x 1 , x 2 là hai giá trị khác nhau của x và y 1 , y 2 là hai giá trị tương ứng của y. Tính x 1 biết x 2 = 3 , y 1 = - 3 / 5 , y 2 = 1 / 10
A. x 1 = - 18
B. x 1 = 18
C. x 1 = - 6
D. x 1 = 6
Vì x và y là hai đại lượng tỉ lệ thuận nên
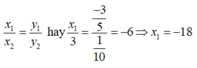
Chọn đáp án A
Đúng 0
Bình luận (0)
Giả sử x và y là hai đại lượng tỉ lệ thuận; x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Tính x1 biết x2 = 3; y1 = -3/5; y2 = 1/10
Giả sử x và y là hai đại lượng tỉ lệ thuận;
x
1
;
x
2
là hai giá trị khác nhau của x và
y
1
;
y
2
là hai giá trị tương ứng của y. Tính
x
1
biết
x
2
3
;
y...
Đọc tiếp
Giả sử x và y là hai đại lượng tỉ lệ thuận; x 1 ; x 2 là hai giá trị khác nhau của x và y 1 ; y 2 là hai giá trị tương ứng của y. Tính x 1 biết x 2 = 3 ; y 1 = ( - 3 / 5 ) ; y 2 = ( 1 / 10 )
A. x 1 = - 18
B. x 1 = 18
C. x 1 = - 6
D. x 1 = 6
Vì x và y là hai đại lượng tỉ lệ thuận nên
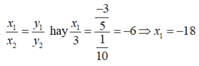
Chọn đáp án A
Đúng 0
Bình luận (0)
Giả sử x và y là hai đại lượng tỉ lệ thuận
x
1
,
x
2
; là hai giá trị khác nhau của x và
y
1
,
y
2
là hai giá trị tương ứng của y. Tính
x
1
,
y
1
biết
2
y
1...
Đọc tiếp
Giả sử x và y là hai đại lượng tỉ lệ thuận x 1 , x 2 ; là hai giá trị khác nhau của x và y 1 , y 2 là hai giá trị tương ứng của y. Tính x 1 , y 1 biết 2 y 1 + 3 x 1 = 24 , x 2 = - 6 , y 2 = 3
A. x 1 = 12 ; y 1 = 6
B. x 1 = - 12 ; y 1 = - 6
C. x 1 = 12 ; y 1 = - 6
D. x 1 = - 12 ; y 1 = 6
Vì x và y là hai đại lượng tỉ lệ thuận nên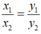 
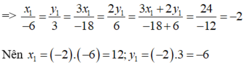
Chọn đáp án C
Đúng 0
Bình luận (0)
giả sử x và y là hai đại lượng tỉ lệ thuận x1 x2 là hai giá trị khác nhau của x và y hai giá trị của y.Tìm x1;y1 biết
y1-3x1=-7,x2=-4,x2=3
giải giúp mình với
28 tháng 12 2021 lúc 20:42
Câu 11: Giả sử x và y là hai đại lượng tỉ lệ thuận x1, x2 là hai giá trị khác nhau của x và y1 ; y2 là hai gía trị tương ứng của y. Tính y1 biết x1 = 5; x2= 4; y2 = 16
\(\dfrac{y_1}{y_2}=\dfrac{x_1}{x_2}=>y_1=20\)
Đúng 0
Bình luận (0)
Câu 2. Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 7 và x2 – 4; y2 3, giá trị của x1; y1 là
A. x1 –28; y1 21;
B. x1 –3; y1 4;
C. x1 –4; y1 3;
D. x1 4; y1 –3.
Đọc tiếp
Câu 2. Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 = 7 và x2 = – 4; y2 = 3, giá trị của x1; y1 là
A. x1 = –28; y1 = 21;
B. x1 = –3; y1 = 4;
C. x1 = –4; y1 = 3;
D. x1 = 4; y1 = –3.
Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ thuận nên đặt $y=ax$.
Ta có:
$y_2=ax_2$
$3=a(-4)\Rightarrow a=\frac{-3}{4}$. Vậy $y=\frac{-3}{4}x$. Thay vào điều kiện $y_1-x_1=7$ ta có:
$\frac{-3}{4}x_1-x_1=7$
$\frac{-7}{4}x_1=7$
$\Rightarrow x_1=-4$
$y_1=7+x_1=7+(-4)=3$
Đáp án C
Đúng 1
Bình luận (0)