Cho \(\Delta\)ABC cân tại A có BC= 1cm; góc A= 200. Vẽ tia Cx trong góc ACB sao cho góc ACx = 100. Tia Cx cắt AB tại M. Tính AM

Những câu hỏi liên quan
\(\Delta ABC\) cân tại B, AH\(\perp\)BC, Biết BH=4cm, CH=1cm. Tính AH, AC
Ta có ΔABC cân tại B ⇒AB=BC=BH+CH=4+1=5(cm)
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH ta có:
\(AH^2+BH^2=AB^2\\ \Rightarrow AH^2=AB^2-BH^2\\ \Rightarrow AH=\sqrt{5^2-4^2}\\ \Rightarrow AH=3\left(cm\right)\)
Áp dụng định lý Pi-ta-go vào tam giác vuông AHC ta có:
\(AH^2+HC^2=AC^2\\ \Rightarrow3^2+1^2=AC^2\\ \Rightarrow AC=\sqrt{10}\left(cm\right)\)
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC. Trên tia đối tia AH lấy điểm D sao cho AD BC. Trên tia đối của tia CA lấy điểm E sao cho AB CE. Đường thẳng vuông góc với BD kẻ từ A cắt BD tại I, cắt DE tại K.1, Chứng minh Delta ABDDelta CEB2, Chứng minh Delta BDEvuông cân3, Tính widehat{CKE}4, Giả sử tam giác ABC vuông cân tại A. Tính DE khi KC 1cm
Đọc tiếp
Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC. Trên tia đối tia AH lấy điểm D sao cho AD = BC. Trên tia đối của tia CA lấy điểm E sao cho AB = CE. Đường thẳng vuông góc với BD kẻ từ A cắt BD tại I, cắt DE tại K.
1, Chứng minh \(\Delta ABD=\Delta CEB\)
2, Chứng minh \(\Delta BDE\)vuông cân
3, Tính \(\widehat{CKE}\)
4, Giả sử tam giác ABC vuông cân tại A. Tính DE khi KC = 1cm
Bài 1:
Cho \(\Delta\)ABC vuông tại A . Đường cao AH chia BC thành 2 phần , HB = 2cm ,HC = 8cm . Tính AH
Bài 2
Cho \(\Delta\)ABC vuông cân tại A có AB =1cm . Tính cạnh huyền BC và đường cao AH
Bài 3
Cho \(\Delta\)ABC có AB =6cm ; BC =7cm ; góc B = 60 độ . Tính AC
1
Áp dụng định lí pi - ta -go , có
+)HB2+AH2=AB2
=>4+AH2=AB2(1)
+)HC2+AH2=AC2
=>64+AH2=AC2(2)
Ta có :CB=CH+HB=8+2=10 (cm) (3)
Từ 1,2 và 3 =>4+AH2+64+AH2=102=100
=>AH2.2=100-68=32
=>AH2=32:2=16=42
=>AH=4
Vậy AH = 4 cm
Cho tam giác ABC cân tại A có AB = 1cm, AC = 23cm. Tính độ dài BC biết độ dài BC là một số nguyên
Giả sử tam giác ABC cân tại B → BA=BC=1 cm
Giả sử tam giác ABC cân tại C → AC=BC= 23cm
Đúng 0
Bình luận (0)
Bài 1:1. Cho DeltaABC vuông tại A. Có AB bằng frac{1}{2}BC. Tính góc C?2. Cho DeltaABC vuông tại A. Có góc B30 độ. C/m ACfrac{1}{2}BC3. Cho DeltaABC. Có trung tuyến BMCN. C/m DeltaABC cân tại A.4. Cho DeltaABC có trung tuyến AM đồng thời là đường phân giác góc A. C/m DeltaABC cân tại A.Giúp mk nhé mai phải nộp rùi!!!
Đọc tiếp
Bài 1:
1. Cho \(\Delta\)ABC vuông tại A. Có AB bằng \(\frac{1}{2}\)BC. Tính góc C?
2. Cho \(\Delta\)ABC vuông tại A. Có góc B=30 độ. C/m AC=\(\frac{1}{2}\)BC
3. Cho \(\Delta\)ABC. Có trung tuyến BM=CN. C/m \(\Delta\)ABC cân tại A.
4. Cho \(\Delta\)ABC có trung tuyến AM đồng thời là đường phân giác góc A. C/m \(\Delta\)ABC cân tại A.
Giúp mk nhé mai phải nộp rùi!!!
Bài 1:
Gọi M là trung điểm của BC
Vẽ BE là tia phân giác của góc B, E thuộc AC
nối M với E
ta có: BM =CM = 1/2.BC ( tính chất trung điểm)
AB=1/2.BC (gt)
=> BM = CM= AB ( =1/2.BC)
Xét tam giác ABE và tam giác MBE
có: AB = MB (chứng minh trên)
góc ABE = góc MBE (gt)
BE là cạnh chung
\(\Rightarrow\Delta ABE=\Delta MBE\left(c-g-c\right)\)
=> góc BAE = góc BME = 90 độ ( 2 cạnh tương ứng)
=> góc BME = 90 độ
\(\Rightarrow BC\perp AM⋮M\)
Xét tam giác BEM vuông tại M và tam giác CEM vuông tại M
có: BM=CM(gt)
EM là cạnh chung
\(\Rightarrow\Delta BEM=\Delta CEM\left(cgv-cgv\right)\)
=> góc EBM = góc ECM ( 2 cạnh tương ứng)
mà góc EBM = góc ABE = 1/2. góc B (gt)
=> góc EBM = góc ABE = góc ECM
Xét tam giác ABC vuông tại A
có: \(\widehat{B}+\widehat{ECM}=90^0\) ( 2 góc phụ nhau)
=> góc EBM + góc ABE + góc ECM = 90 độ
=> góc ECM + góc ECM + góc ECM = 90 độ
=> 3.góc ECM = 90 độ
góc ECM = 90 độ : 3
góc ECM = 30 độ
=> góc C = 30 độ
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a có bc=5\(\sqrt{2}\)và đường tròn nội tiếp \(\Delta ABC\)có bán kính=1cm . tìm dt abc
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A có AC1cm, BC2cm. Kẻ đường trung tuyến BK và đường cao AHa) Tính ABb) Tính BK và AH2. Cho tam giác ABC vuông cân tại A (ˆBAC90BAC^90 độ, BDBA). Ở phía ngoài tam giác ABC, dựng tam giác DAB vuông cân tại D (ˆDAB90DAB^90 độ, BDBA). Gọi E là một điểm tùy ý trên DA. Đường thẳng đi qua E và vuông góc với BE cắt AC ở Fa) Gọi K là giao điểm của BD và AC. CMR tam giác KAB vuông cân tại A và DA là đường trung trực của đoạn KBb) CMR tam giác KEA tam giác BEAc) CMR tam giác K...
Đọc tiếp
1. Cho tam giác ABC vuông tại A có AC=1cm, BC=2cm. Kẻ đường trung tuyến BK và đường cao AH
a) Tính AB
b) Tính BK và AH
2. Cho tam giác ABC vuông cân tại A (ˆBAC=90BAC^=90 độ, BD=BA). Ở phía ngoài tam giác ABC, dựng tam giác DAB vuông cân tại D (ˆDAB=90DAB^=90 độ, BD=BA). Gọi E là một điểm tùy ý trên DA. Đường thẳng đi qua E và vuông góc với BE cắt AC ở F
a) Gọi K là giao điểm của BD và AC. CMR tam giác KAB vuông cân tại A và DA là đường trung trực của đoạn KB
b) CMR tam giác KEA= tam giác BEA
c) CMR tam giác KEF cân tại E. Từ đó suy ra BE= EF
Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta \)BAM = \(\Delta \)CAN;
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
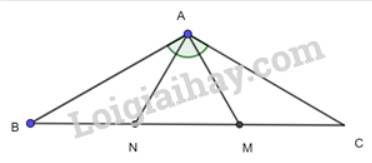
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC= 1cm; AC= 7cm và độ dài cạnh AB là một số nguyên (cm).Tính độ dài AB và cho biết tam giác ABC là tam giác gì?
A. AB= 7cm và tam giác ABC vuông tại A
B. AB= 7cm và tam giác ABC cân tại A
C. AB= 7cm và tam giác ABC vuông cân tại A
D. AB= 8cm và tam giác ABC vuông tại B
Xem thêm câu trả lời

























