Cho hàm số y = f(x) có đồ thị là (C). Xét điểm M(x; f(x)) thay đổi trên (C). Biết rằng, hệ số góc của tiếp tuyến của đồ thị (C) tại M là kM = (x – 1)2 và điểm M trùng với gốc tọa độ khi nó nằm trên trục tung. Tìm biểu thức f(x).
Những câu hỏi liên quan
cho đồ thị hàm số y = f (x) = 2x-2
a) Tính f (0) : f(1): F( -1)
b) xét xem điểm nào thuộc đồ thị hàm số trên A ( 0; -2) : B( -1; 1)
c) cho điểm C ( m;2) thuộc đồ thị hàm số . Hãy tìm m
a, \(f(0)\)= -2
\(f(1) \)=0
\(f(-1) \)=-4
b,A(0;2)
c,m =2
a)
f(0) = 2 . 0 - 2 = -2
f(1) = 2.1 - 2 = 0
f(-1)= 2.(-1) - 2 = -4
b) Thay tọa độ A,B vào phương trình đồ thị hàm số ta có :
A : -2 = 2. 0 - 2 đúng=> A \(\in\)u= 2x -2
B: 1 = 2 . (-1) - 2 sai => B \(\in\)y =2x - 2
c) \(C\in y=2x-2\Rightarrow2=2m-2\Leftrightarrow m=2\)
Cho đồ thị hàm số y=f(x)=2x-2
a) tính f(0), f(1), f(-1)
b) xét xem điểm nào thuộc đồ thị hàm số trên A(0;-2) B(-1;1)
c) cho điểm C(m;2) thuộc đồ thị hàm số. Hãy tìm m
Cho hàm số y=f(x) xác định trên R và có bảng xét dấu đạo hàm như sau:
Khi đó số điểm cực trị của đồ thị hàm số y=f(x) là
A. 3
B. 2
C. 4
D. 1
Chọn A.
Tại các điểm x 1 , x 2 , x 3 hàm số y=f(x) xác định và hàm số y=f’(x) không xác định hoặc bằng 0, ngoài ra hàm số y=f’(x) còn đổi dấu qua các điểm đó nên hàm số y=f(x) có 3 điểm cực trị.
Đúng 0
Bình luận (0)
Các bạn giải hộ mình câu hỏi này được không
Cho hàm số y=f (x) = 3x
a) Tính (-2) , f(0)?
b)Vẽ đồ thị hàm số trên
c) Xét xem các điểm sau có thuộc đồ thị hàm số đó không A (3,9)
d) Cho điểm C (m,-6) thuộc đồ thị hàm số trên. Tìm m
a . ta có \(f\left(-2\right)=3\times\left(-2\right)=-6\)
\(f\left(0\right)=3\times0=0\)
b. Vẽ đồ thị hàm số 
c. ta có \(f\left(3\right)=3\times3=9\) nên điểm A( 3,.9) thuộc đồ thị hàm số.
d. Xét \(f\left(m\right)=3\times m=-6\Leftrightarrow m=-2\)
vậy m= -2 thì điểm C thuộc đồ thị hàm số
Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 12:54
Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.
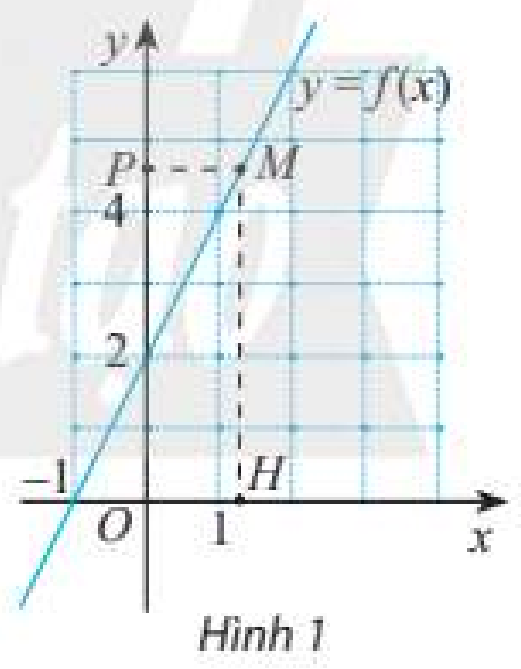
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).
Đúng 0
Bình luận (0)
Cho hai hàm đa thức y f(x), y g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y f(x) có đúng một điểm cực trị là A, đồ thị hàm số y g(x) có đúng một điểm cực trị là B và
A
B
7
4
.
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số
y
f
(
x
)...
Đọc tiếp
Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là A, đồ thị hàm số y = g(x) có đúng một điểm cực trị là B và A B = 7 4 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số y = f ( x ) - g ( x ) + m có đúng 5 điểm cực trị?
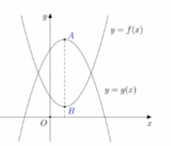
A. 1
B. 3
C. 4
D. 6
cho hàm số y+ f(x) + (m-1)*x (m khác 1.
a. xét công thức đã cho biết đồ thị hàm số đó đi qua điểm A(1;3)
b. tính f(-1); f(-1/2)
c. tìm x để f(x)=-5; f(x)=-4
d. vẽ đồ thị hàm số đã cho
e. trong các điểm B(-2:4) D(-1;-3); e(1/3;1) điểm nào thuộc đò thị đã cho
Cho hàm số y f(x) có đồ thị hàm số y f (x) như hình vẽ. Xét hàm số
g
x
2
f
x
+
2
x
3
-
4
x
-
3
m
-
6
5
với m là số thực. Để
g
x
≤
0
,
∀
x
∈
-
5...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị hàm số y = f '(x) như hình vẽ. Xét hàm số g x = 2 f x + 2 x 3 - 4 x - 3 m - 6 5 với m là số thực. Để g x ≤ 0 , ∀ x ∈ - 5 ; 5 thì điều kiện của m là
A. m ≥ 2 3 f 5
B. m ≤ 2 3 f 5
C. m ≤ 2 3 f 0 - 2 5
D. m ≥ 2 3 f - 5 - 4 5
Đáp án A
Ta có g x = 2 f x + 2 x 3 - 4 x - 3 m - 6 5 ≤ 0 , ∀ x ∈ - 5 ; 5
⇔ h x = 2 f x + 2 x 3 - 4 x - 6 5 ≤ 3 m , ∀ x ∈ - 5 ; 5 ⇔ m a x - 5 ; 5 h x ≤ 3 m
Mặt khác h ' x = 2 f ' x + 6 x 2 - 4 = 0 ⇔ f ' x = 2 - 3 x 2
Dựa vào đồ thị f '(x) ta thấy rằng phương trình f ' x ≥ 2 - 3 x 2 , ∀ x ∈ - 5 ; 5
Do đó h(x) đồng biến trên đoạn - 5 ; 5
Suy ra h 5 = 2 f 5 ≤ 3 m ⇔ m ≥ 2 3 f 5 .
Đúng 0
Bình luận (0)
câu 1: cho hàm số yax+bXác định giá trị a và b biết đồ thị hàm số đi qua điểm M; m(2;5) và N(1/3;0)câu 2: cho hàm số:yf(x)-2x; g(x)x-1a, tính f(3); g(-2)b, tìm tung độ của điểm A thuộc đồ thị hàm số của điểm A thuộc đồ thị hàm số f(x) có hoành độ là 1/2c.tính hoành độ của điểm B thộc đồ thị hàm số g(x)có tung độ là -3d, điểm C(1/3;-2/3) có thuộc đồ thị hàm số f(x); g(x) không
Đọc tiếp
câu 1: cho hàm số y=ax+b
Xác định giá trị a và b biết đồ thị hàm số đi qua điểm M; m(2;5) và N(1/3;0)
câu 2: cho hàm số:y=f(x)=-2x; g(x)=x-1
a, tính f(3); g(-2)
b, tìm tung độ của điểm A thuộc đồ thị hàm số của điểm A thuộc đồ thị hàm số f(x) có hoành độ là 1/2
c.tính hoành độ của điểm B thộc đồ thị hàm số g(x)có tung độ là -3
d, điểm C(1/3;-2/3) có thuộc đồ thị hàm số f(x); g(x) không
Xác định hệ số a, biết rằng đồ thị của hàm số y=ax đi qua điểm A(6;2).Điểm B(-9;3), điểm C(7;-2) có thuộc đồ thị hàm số không ? Tìm trên đồ thị của hàm số điểm D có hoành độ bằng -4,điểm E có tung độ bằng 2
Đúng 0
Bình luận (0)
Xét các khẳng định sau:(I). Nếu hàm số y f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M m (II). Đồ thị hàm số
y
a
x
4
+
b
x
2
+
c
(
a
≠
0...
Đọc tiếp
Xét các khẳng định sau:
(I). Nếu hàm số y = f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M > m
(II). Đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III). Tiếp tuyến (nếu có) tại một điểm cực trị của đồ thị hàm số luôn song song với trục hoành.
Số khẳng định đúng là :
A. 0
B. 3
C. 2
D. 1
Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
(I) sai. Ví dụ hàm số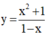 
có đồ thị hàm số như sau:
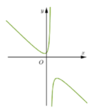õ ràng 
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số 
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: 
luôn song song với trục hoành.
Vậy (III) đúng.
Đúng 0
Bình luận (0)