Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; S A ⊥ A B C D và S A = 2 a . Tính khoảng cách d từ điểm B đến mặt phẳng (SCD).
A. d = a 5 5 .
B. d = a .
C. d = 4 a 5 5 .
D. d = 2 a 5 5 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy (ABCD) và S C = a 5 . Tính thể tích khối chóp S.ABCD
A. V = a 3 3 3 .
B. V = a 3 3 6 .
C. V = a 3 3 .
D. V = a 3 15 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy A B C D và S C = a 5 . Tính thể tích khối chóp S.ABCD.
A. V = a 3 3 3 .
B. V = a 3 3 6 .
C. V = a 3 3 .
D. V = a 3 15 3 .
Đáp án A
Tam giác SAC vuông tại A suy ra:
S A = S C 2 − A C 2 = a 5 2 − a 2 2 = a 3
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 . S A . S S . A B C D = 1 3 . a 3 . a 2 = a 3 3 3
1. cho hình chóp S.ABCD có đáy ABCD là hình vuông. Số mặt bên của hình chóp là? Kể tên
2. cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Số cạnh đáy của hình chóp là? Kể tên
3. cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Vị trí tương đối giữa 2 đường thẳng SA và BC là
4. hình tứ diện ABCD có bao nhiêu đỉnh? Kể tên
5. hình chóp S.ABCD có bao nhiêu mặt. Kể tên
6. các yếu tố nào sau đây xác định 1 mặt phẳng duy nhất
A. ba điểm phân biệt
B. 1 điểm và 1 đường thẳng
C. 2 đường thẳng cắt nhau
D. 4 điểm phân biệt
1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 3 . Tính thể tích hình chóp S.ABCD.
A. a 3 3
B. a 3 3 3
C. a 3 3
D. 3 a 3 3
Phương pháp:
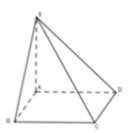
Thể tích khối chóp có chiều cao h và diện tích đáy S là ![]()
Cách giải:
Diện tích đáy ![]()
Thể tích khối chóp là
![]()
Chọn B.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 3 . Tính thể tích hình chóp S.ABCD
A. a 3 3
B. a 3 3 3
C. a 3 3
D. 3 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 3 . Tính thể tích hình chóp S.ABCD
A. a 3 3
B. a 3 3 3
C. a 3 3
D. 3 a 3 3
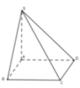
Diện tích đáy S A B C D = a 2
Thể tích khối chóp là
V A B C D = 1 3 S A . S A B C D = 1 3 . a 3 . a 2 = a 3 3 3
Chọn đáp án B.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD), SA=2a. Tính theo a thể tích khối chóp S.ABCD
A. a 3 3
B. a 3 6
C. a 3 4
D. 2 a 3 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA vuông góc với (ABCD) và Thể tích của khối chóp S.ABCD là:

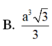
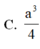
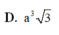
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. S A ⊥ A B C D và S B = a 3 . Thể tích khối chóp S.ABCD là
A. a 3 2 4
B. a 3 2 2
C. a 3 2 6
D. a 3 2 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên S A = a 6 và vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD
A. 8 πa 2
B. 2 πa 2
C. 2 a 2
D. a 2 2