Cho tam giác ABC. D,E,F lần lượt là trung điểm của các cạnh AB, BC, AC và O là giao điểm các đường trung trực của tam giác ABC. Cho OD > OE; OE = OF. Hãy sao sánh BC và AC; AB và AC

Những câu hỏi liên quan
Cho tam giác ABC, O là giao của các đường trung trực của tam giác; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, AC. Cho biết OD > OE, OE = OF (h.69).
Hãy so sánh các độ dài:
BC và AC;
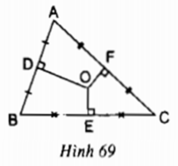
O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
OE = OF ⇒ AC = BC
Đúng 0
Bình luận (0)
Cho tam giác ABC, O là giao của các đường trung trực của tam giác; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, AC. Cho biết OD > OE, OE = OF (h.69).
Hãy so sánh các độ dài:
AB và AC
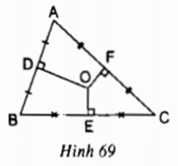
O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
OD > OE ⇒ AB < AC
Đúng 0
Bình luận (0)
Cho tam giác ABC, O là giao của các đường trung trực của tam giác; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, AC. Cho biết OD > OE, OE = OF (h.69).
Hãy so sánh các độ dài:
a) BC và AC;
b) AB và AC.
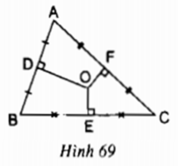
O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
a) OE = OF ⇒ AC = BC
b) OD > OE ⇒ AB < AC
Đúng 0
Bình luận (0)
1)CHO TG ABC VUÔNG TẠI A.VẼ AH VUÔNG VỚI BC TẠI H.TIA PHÂN GIÁC GÓC HAB CẮT BC TẠI D.TIA PHÂN GIÁC GÓC HAC CẮT BC TẠI E.CM: GIAO ĐIỂM CÁC ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC ABC LÀ GIAO ĐIỂM CÁC ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC ADE.2)CHO TAM GIÁC ABC CÓ ACAB.TRÊN CA LẤY E SAO CHO CEAB.CÁC ĐƯỜNG TRUNG TRỰC CỦA BE VÀ AC CẮT NHAU TẠI O.CM:A)TAM GIÁC AOBTAM GIÁC AOCB)AO LÀ TIA PHÂN GIÁC CỦA GÓC BAC3)CHO TAM GIÁC ABC ĐỀU.TRÊN AB,BC,AC LẤY CÁC ĐIỂM D,E,F SAO CHO ADBECF.CM:A)TAM GIÁC DEF ĐỀU.B)GỌI O LÀ GIAO ĐIỂM...
Đọc tiếp
1)CHO TG ABC VUÔNG TẠI A.VẼ AH VUÔNG VỚI BC TẠI H.TIA PHÂN GIÁC GÓC HAB CẮT BC TẠI D.TIA PHÂN GIÁC GÓC HAC CẮT BC TẠI E.
CM: GIAO ĐIỂM CÁC ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC ABC LÀ GIAO ĐIỂM CÁC ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC ADE.
2)CHO TAM GIÁC ABC CÓ AC>AB.TRÊN CA LẤY E SAO CHO CE=AB.CÁC ĐƯỜNG TRUNG TRỰC CỦA BE VÀ AC CẮT NHAU TẠI O.
CM:A)TAM GIÁC AOB=TAM GIÁC AOC
B)AO LÀ TIA PHÂN GIÁC CỦA GÓC BAC
3)CHO TAM GIÁC ABC ĐỀU.TRÊN AB,BC,AC LẤY CÁC ĐIỂM D,E,F SAO CHO AD=BE=CF.
CM:A)TAM GIÁC DEF ĐỀU.
B)GỌI O LÀ GIAO ĐIỂM CÁC ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC ABC.CM:Ó CŨNG LÀ GIAO ĐIỂM CÁC ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC DEF
mau lên giùm mình đê các bạn ơi.mau,mau đê
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
b) Chứng I là trung điểm của DF.
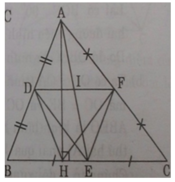
b) Ta có DF // BC (cmt) hay DI // BE; D là trung điểm của AD ⇒ I là trung điểm của AE và DI = BE/2
Trong ΔAEC có IF là đường trung bình nên IF = EC/2 mà EC = EB (gt) ⇒ IF = ID hay I là trung điểm của DF.
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, AD là đường cao. Vẽ các điểm M, N sao cho AB là trung trực của DM, AC là trung trực của DN. Gọi E, F lần lượt là giao điểm của MN với AC, AB. CMR: a) Tam giác AMN cân b) DE+EF+DF=MN c) DA là phân giác góc EDF d) Giao điểm các đường phân giác của tam giác DEF và trực tâm tam giác ABC trùng nhau
tự kẻ hình nha:333
a) vì AB là trung trực của DM=> MH=HD( đặt H là giao điểm của AB và DM)
xét tam giác MAB và tam giác DAB có
MH=HD(cmt)
AHM=AHD(=90 độ)
AH chung
=> tam giác MAB= tam giác DAB(cgc)
=> AM=AD( hai cạnh tương ứng)
vì AC là trung trực của DN=> NK=DK( đặt K là giao điểm của AC và DN)
xét tam giác AKD và tam giác AKN có
DK=NK(cmt)
AKD=AKN(=90 độ)
AK chung
=> tam giác AKD= tam giác AKN( cgc)
=> AN=AD ( hai cạnh tương ứng)
AM=AD(cmt)
=> AM=AN=> tam giác AMN cân A
b) vì E thuộc đường trung trực AB=> EM=ED
vì F thuộc đường trung trực AC=> FD=FN
ta có MN=ME+EF+FN mà EM=ED, FD=FN
=> MN= ED+EF+FD
c) xét tam giác ADF và tam giác ANF có
FD=FN(cmt)
AD=AN(cmt)
AF chung
=> tam giác ADF= tam giác ANF(ccc)
=> ANF=ADF( hai góc tương ứng)
xét tam giác AME và tam giác ADE có
AM=AD(cmt)
AE chung
EM=ED(cmt)
=> tam giác AME= tam giác ADE(ccc)
=> AME=ADE( hai góc tương ứng)
mà AME=ANF( tam giác AMN cân A)
=> ADE=ADF=> AD là p/g của EDF
d) chưa nghĩ đc :)))))))
CHUẨN R BN ƠI HỌC THÌ NGU MÀ CHƠI NGU THÌ GIỎI
Cho tam giác ABC đều. Trên các cạnh AB, BC, AC lấy 3 điểm theo thứ tự D, E, F sao cho AD=BE=CF
a) CMR tam giác DEF đều
b) Gọi O là giao điểm các dường trung trưc của tam giác ABC. CMR O cũng là giao điểm các đường trung trực của tam giác DEF
cho t/g ABC có AB=BC Trên các cạnh AB, AC lấy lần lượt các điểm D và E sao cho AD=AE
Gọi O là giao điểm của BE và CD. Chứng minh rằng:
a,tam giác abe=acd
b,od=oe,ob=oc
cho t/g ABC có AB=BC Trên các cạnh AB, AC lấy lần lượt các điểm D và E sao cho AD=AE
Gọi O là giao điểm của BE và CD. Chứng minh rằng:
a,tam giác abe=acd
b,od=oe,ob=oc
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Đúng 0
Bình luận (0)











