b) Ta có DF // BC (cmt) hay DI // BE; D là trung điểm của AD ⇒ I là trung điểm của AE và DI = BE/2
Trong ΔAEC có IF là đường trung bình nên IF = EC/2 mà EC = EB (gt) ⇒ IF = ID hay I là trung điểm của DF.
Cho tam giác ABC từ điểm D trên cạnh BC kẻ các đường thẳng de df lần lượt song song với AB AC Gọi K là trung điểm của AB E là trung điểm của bc i là giao điểm của AD và HK Chứng minh rằng
a) tứ giác aedf là hình bình hành
b) và F đối xứng với nhau qua điểm I
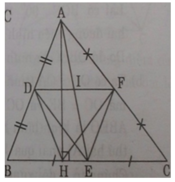
cho tam giác abc nhọn , đường cao ah . gọi D,E,F lần lượt là trung điểm của các cạnh BC,CA,AB .c/m
a, DE=HF,DF=HE
b, gọi o là giao điểm của DF và HE . c/m o thuộc đường trung trực cua EF
cho tam giác ABC vuông tại A .Từ trung điểm D của cạnh BC kẻ DE,DF lần lượt vuông góc với AB,AC(E thuộc AB,F thuộc AC)
a)Chứng minh:AEDF là hình chữ nhật
b)Gọi I là điểm đối xứng của D qua E.Chứng minh:tứ giác AIBD là hình thoi
c)Gọi O là trung điểm của EF.Chứng minh:ba điểm I,O,C thảng hàng
MỌI NGƯỜI GIÚP MÌNH BÀI NÀY VỚI,CHO MÌNH XIN CÁI HÌNH CỦA BÀI NÀY VỚI LẠI GIÚP MINH CÂU B VÀ C LUÔN Ạ
cho tam giác ABC co đường cao AD vẽ các điểm E và F sao cho AB, AC lần lượt là đường trung trực của DE và DF gọi giao điểm của È với AB và AC lần lượt là K và I
Chứng minh AD, CK, BI thẳng hàng
Bài1:Cho tam giác ABC,M là điểm nằm trong tam giác. Gọi D là giao điểm của AM và BC, E là giao điểm của BM và CA. F là giao điểm của CM và AB, đường thẳng đi qua M và song song với BC cắt DE, DF lần lượt tại K và I. Cmr MI=MK.
Bài 2:Cho tam giác ABC, các đường trung tuyến BM, CN cắt nhau tại G, K là điểm trên cạnh BC, đường thẳng đi qua K và song song CN cắt AB ở D, đường thẳng đi qua K và song song với BM cắt AC ở E. Gọi I là giao điểm của KG và DE. Cmr I là trung điểm của DE.
Bài 3:Cho tam giác ABC đều. Gọi M, N là các điểm trên AB, BC sao cho BM=BN. Gọi G là trọng tâm của tam giác BMN. I là trung điểm của AN, P là trung điểm của MN.Cmr:
a, tam giác GPI và tam giác GNC đồng dạng.
b, IC vuông góc với GI.
Bài 4:Cho tam giác ABC vuông tại A, đường cao AH. I là trung điểm của AC, F là hình chiếu của I trên BC. Trên nửa mặt phẳng bờ là đường thẳng chứa AC, vẽ Cx vuông góc với AC cắt IF tại E. Gọi giao điểm của AH, AE với BI theo thứ tự G và K. Cmr:
a,Tam giác IHE và tam giác BHA đồng dạng.
b, Tam giác BHI và tam giác AHE đồng dạng.
c, AE vuông góc với BI.
LÀM ƠN HÃY GIÚP MÌNH NHA. MÌNH ĐANG RẤT VỘI. THANK KIU CÁC BẠN!!!😘😘😘
Cho tam giác ABC (AB < AC), đường cao AK. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. a,Tứ giác BDEF là hình gì ? Vì sao ? b,Chứng minh tứ giác DEFK là hình thang cân. c) Gọi I là giao điểm BE và DF, H là điểm đối xứng của E qua C/m IC//BH
cho tam giác ABC vuông tại A.Từ trung điểm D của cạnh BC kẻ DE,DF lần lượt vuông góc với AB,AC(E thuộc AB,F thuộc AC)
a)Chứng minh:tứ giác AEDF là hình chữ nhật
b)Gọi I là điểm đối xứng của D qua E.Chứng minh:tứ giác AIBD là hình thoi
c)Gọi O là trung điểm của EF.Chứng minh ba điểm I,O,C thẳng hàng
CÁC BẠN GIÚP M,ÌNH BÀI NÀY VỚI Ạ,GHI RÕ RÕ GIÚP MÌNH LUÔN NHÉ,MÌNH CẢM ƠN
B1, cho tam giác abc, d là một điểm trên cạnh BC. Qua D kẻ đường thẳng // với AB cắt AC ở E. Trên AB lấy điểm F sao cho AF=DE. Gọi I là trung điểm của AD. CMR:
a,DF=AE
b,E và F đối xứng nhau qua I
B2, Cho hbh ABCD lấy E và F lần lượt là trung điểm Ab và CD,lấy M thuộc tia đối của tia AD sao cho AM=AD. CM các tứ giác sau là hbh:
a,Tứ giác AEFD
b,Tứ giác AMEF
c,Tứ giác AMBC
Cho tam giác ABC , định trên cạnh AB và AC các điểm D và E sao cho BD = CE . Gọi M là trung điểm của DE , N là trung điểm của BC . I và F lần lượt là giao điểm của MN với AC và AB . Chứng minh tam giác AIF cân
