Cho tam giác ABC vuông tại A . M nằm trong tam giác sao cho MA=2cm ; MB=3cm và góc AMC = 135 độ . Tính MC
cho tam giác ABC vuông cân tại đỉnh A. M là một điểm nằm trong tam giác ABC, MA=2cm,MB=3cm, góc AMC= 135 độ. Tính độ dài đoạn thẳng MC
\(\left(1\right)\Delta ABC\) vuông cân tại A. M là 1 điểm nằm trong tam giác ABC. Sao cho MA= 2cm , MB = 3cm , góc AMC = 135o . Tính MC
(2) Tam giác ABC vuông cân tại A . M là 1 điểm nằm trong tam giác ABC. Sao cho MC : MA : MB = 1:2:3 . Tính góc AMC
Mong được mấy anh chị CTV hoặc quản lí giúp đỡ ạ!
Cho tam giác ABC vuông cân tại A. Điểm M nằm bên trong tam giác sao cho MA=2cm, MB=3cm, và \(\widehat{AMC}\)=135. Tính MC
Ai làm được mk tk 3 tk và kb luôn
bài 1 )
cho hình tam giác vuông tại A, m nằm trong tam giác sao cho MA=2cm, MB=3cm, góc AMC=135 độ. Tính MC
bài 2 )
cho hình tam giác ABC vuông tại A có góc B = 60 độ. trên tia BA lấy E sao cho BE=BC. tia phân giác góc B cắt AC tại I
câu a) chứng minh: IE=IA
câu b) chứng minh IE vuông góc BC
Cho tam giác ABC vuông cân tại A và điểm M nằm trong tam giác sao cho MA=1, MB=2, MC= 2 . Tính góc A M C ⏜
![]()
![]()
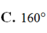
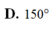
giải giúp mik vs
Điểm M nằm bên trong tam giác vuông cân ABC tại B sao cho MA = 1cm, MB = 2cm, MC = 3cm. Tính góc AMB.
Cho \(\Delta ABC\)vuông cân tại A. Điểm M nằm trong tam giác sao cho MA=2cm, MB=3cm và \(\widehat{AMC}\)=135. Tính MC
trên nửa mặt phẳng bờ AM không chứa điểm B vẽ tam giác ADM vuông cân tại A
Ta có : \(\widehat{DMC}=\widehat{AMC}-\widehat{AMD}=90^o\)
\(\Rightarrow\)\(\Delta ADC=\Delta AMC\left(c.g.c\right)\)
\(\Rightarrow\)DC = MB = 3cm
Xét \(\Delta AMD\)vuông tại A, theo định lí Py-ta-go, ta có :
MD2 = MA2 + AD2 = 22 + 22 = 8
Xét \(\Delta MCD\)vuông tại M , theo định lí Py-ta-go, ta có :
CD2 = MD2 + MC2 \(\Rightarrow\)MC2 = CD2 - MD2 \(\Rightarrow\)MC2 = 32 - 8 = 1 \(\Rightarrow\)MC = 1 cm
Cho tam giác ABC vuông cân tại A. M nằm bên trong tam giác sao cho MA, MB, MC tỉ lệ với 2,3,1. Tính góc AMC?
Cho tam giác ABC Có góc B = 75 độ, góc C = 60 độ. Điểm M nằm trong tam giác ABC sao cho tam giác MBC vuông cân tại M. CMR: MA =MB
Mk chỉ chứng minh chứ hông vẽ hình đâu nha !!!
C/m:
Từ giả thiết ta có:
\(\widehat{BAC}=180^0-\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-\left(75^0+60^0\right)=45^0\) \(\left(.\right)\)
\(\widehat{B}_2=\widehat{ABC}-\widehat{B_1}=75^0-45^0=30^0\)
\(\widehat{C}_2=\widehat{ACB}-\widehat{C_1}=60^0-45^0=15^0\)
Giả sử \(MA\ne MB\)ta xét 2 trường hợp:
T/ hợp 1: \(MA< MB\)
Xét \(\Delta MAB,\)vì \(MA< MB\)nên \(\widehat{B_2}< \widehat{A}_2\)
Nối MA.
Để chứng minh MA =MB. Ta dùng phản chứng.
G/s: \(MA\ne MB\)
Vì tam giác MBC vuông cân => MB=MC và \(\widehat{MCB}=\widehat{MBC}=45^o\)
Xét tam giác ABC có: \(\widehat{ACB}=60^o;\widehat{ABC}=75^o\)=> \(\widehat{CAB}=180^o-60^o-75^o=45^o\)
Vì M nằm trong tam giác ABC => \(\widehat{ACM}=\widehat{ACB}-\widehat{MCB}=60^o-45^o=15^o\)và \(\widehat{ABM}=\widehat{ABC}-\widehat{MBC}=75^o-45^o=30^o\)
+) TH1: MA> MB=MC
Xét tam giác MAB có: MA >MB => ^MAB < ^MBA => \(\widehat{MAB}< 30^o\)
Xét tam giác MAC có: MA >MC => ^MAC < ^MCA => \(\widehat{MAC}< 15^o\)
=> \(\widehat{BAC}=\widehat{BAM}+\widehat{CAM}< 30^o+15^o\Rightarrow\widehat{BAC}< 45^o\)(vô lí)
+) TH1: MA< MB=MC
Xét tam giác MAB có: MA <MB => ^MAB > ^MBA => \(\widehat{MAB}>30^o\)
Xét tam giác MAC có: MA <MC => ^MAC > ^MCA => \(\widehat{MAC}>15^o\)
=> \(\widehat{BAC}=\widehat{BAM}+\widehat{CAM}>30^o+15^o\Rightarrow\widehat{BAC}>45^o\)(vô lí)
=> Điều giả sử là sai
=> MA=MB
Làm tiếp nè:
Xét \(\Delta MAB,\)vì \(MA< MB\)nên \(\widehat{B_2}< \widehat{A_2}\)( quan hệ góc - cạnh đối diện )
Vì \(MC=MB\)nên \(MA< MC\)
Do đó: \(\widehat{C_2}< \widehat{A_1}\) ( quan hệ góc - cạnh đối diện trong \(\Delta MAC\))
Suy ra: \(\widehat{B}_2+\widehat{C_2}< \widehat{A_1}+\widehat{A_2}\)hay \(30^0+15^0=45^0< \widehat{BAC}\): trái với \(\left(.\right)\)
T/hợp 2: \(MA>MB\)
Xét \(\Delta MAB,\)vì \(MA>MB\)nên \(\widehat{B_2}>\widehat{A_2}\)( quan hệ góc - cạnh đối diện )
Vì \(MC=MB\)nên \(MA>MC\)
Dó đó: \(\widehat{C_2}>\widehat{A_1}\) ( quan hệ góc - cạnh đối diện trong \(\Delta MAC\))
Suy ra: \(\widehat{B}_2+\widehat{C_2}>\widehat{A_1}+\widehat{A_2}\)hay \(30^0+15^0=45^0>\widehat{BAC}\): trái với \(\left(.\right)\)
Vậy điều giả sử \(MA\ne MB\)là sai, hay \(MA=MB\)
Bài làm của mk hay của Cô Linh Chi đều đc nha !
cho tam giác ABC vuông cân tại A. M nằm trong tam giác ABC sao cho : BM=BA và góc ABM=36 độ. chứng minh rằng: MA=MC. ( chứng minh bằng 2 cách)