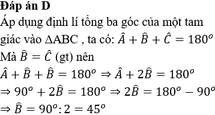cho tam giác ABC , góc A = 90o; I , K thuộc AC sao cho AI=IK=KC . Lấy H;M là trung điểm của BI,BC
a) CM: tứ giác HMCA là hình thang
b) CM: tứ giác HMKA là hình thang cân

Những câu hỏi liên quan
Cho tam giác ABC có góc A 90o. Kẻ AH vuông góc với BC. Các tam giác AHC và BAC có AC cạnh chung, góc C là góc chung, góc AHC góc BHC 90o nhưng hai tam giác này không bằng nhau. Tại sao ở đây không thể áp dụng trường hợp góc - cạnh góc để kết luận tam giác AHC tam giác BAC
Đọc tiếp
Cho tam giác ABC có góc A = 90o. Kẻ AH vuông góc với BC. Các tam giác AHC và BAC có AC cạnh chung, góc C là góc chung, góc AHC = góc BHC = 90o nhưng hai tam giác này không bằng nhau.
Tại sao ở đây không thể áp dụng trường hợp góc - cạnh góc để kết luận tam giác AHC = tam giác BAC
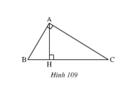
Hai tam giác AHC và BAC có:
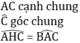
Nhưng hai tam giác này không bằng nhau vì góc AHC không phải là góc kề với cạnh AC
Đúng 0
Bình luận (0)
Cho tam giác ABC và tam giác MNP có
A
^
M
^
90
o
;
C
^
P
^
. Cần thêm một điều kiện gì để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông - góc nhọn kề? A. AC MP B. AB MN C. BC NP D. AC MN
Đọc tiếp
Cho tam giác ABC và tam giác MNP có A ^ = M ^ = 90 o ; C ^ = P ^ . Cần thêm một điều kiện gì để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông - góc nhọn kề?
A. AC = MP
B. AB = MN
C. BC = NP
D. AC = MN
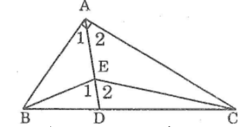
Cho tam giác ABC có ∠A =90o. Gọi E là điểm nằm trên tam giác đó. Chứng minh rằng góc BEC là góc tù.
Kéo dài AE cắt BC tại D
Trong ∆ABE ta có ∠E1 là góc ngoài tại đỉnh E
Suy ra: ∠E1 > ∠A1 (tính chất góc ngoài tam giác)(1)
Trong ∆AEC ta có ∠E2 là góc ngoài tại đỉnh E
Suy ra: ∠E2 > ∠A2 (tính chất góc ngoài tam giác)(2)
Cộng từng vế (1) và (2) ta có:
∠E1 + ∠E2 > ∠A1 +∠A2
Hay ∠ (BEC) > ∠ (BAC) = 90º
Vậy góc (BEC) là góc tù.
Đúng 0
Bình luận (0)
Cho tam giác ABC, M là trung điểm của BC
CMR: a, Nếu AM=BC/2 thì góc A=90o
b, Nếu góc A=90o thì AM=BC/2
Cho tam giác ABc, có A=90o. Tia phân giác BE của góc ABC( E thuộc AC). Trên BC lấy sao cho BM=BA.
a)CM: tam giác BEA= tam giác BEM
b) CM: EM vuông góc với BC
c) So sánh góc ABC và góc MEC
a) Xét tam giác BEA và tam giác BEM ta có:
BA=BM (gt)
góc ABE=góc MBE (gt)
BE là cạnh chung
=> tam giác BEA=tam giác BEM ( c-g-c)
b) Vì tam giác BEA= tam giác BEM
=> góc BME= góc BAE (góc tương ứng)
=>góc BME= 90* (góc BAE=90*)
=>EM vuông góc BC
c) ta có :
góc BME+góc EMC= 180*(kề bù)
=>90*+EMC=180*
=>EMC=90*
Mặt khác:
ABC=90*-C
Ta Có
EMC+MCE+MEC=180*
=> 90*+MCE+MEC=180*
=>C+MEC=90*
=>MEC=90*-C
=>ABC=MEC=90*-C
Vậy ABC=MEC
Đúng 0
Bình luận (0)
Cho tam giác ABC có A ^ = 90 o , B ^ = C ^ . Tính số đo góc B
A. 90 °
B. 90 °
C. 90 °
D. 90 °
Cho tam giác ABC có góc A = góc B + góc C. Hai đường phân giác của góc A và góc C cắt nhau tại O. Góc BOC bằng:
90o
85o
150o
135o
`hatA+hatB+hatC=180^o`
mà `hatA=hatB+hatC `
`=>hatA+hatA=180^o`
`=>2hatA=180^o`
`=>hatA=90^o`
`+)hat{BOC}=180- (hat{OBC}+hat{OCB})`
.vì o là giao điểm của 3 đường phân giác
`=>2(hat{BOC}+hat{OCB})=hatA=90^o`
`=>hat{BOC}=180^o-90^o/2=180^o-45^o=135^o`
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A = 90o, AH vuông góc với CB, biết góc B = 30o, AH = 6 cm. Tính các cạnh của tam giác ABC
mik cảm ơn nhiều ạ!!!
Cho tam giác ABC có ∠A=90o, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác của ∠C và ∠BAH cắt nhau ở I. Chứng minh rằng: ∠(AIC)=90o
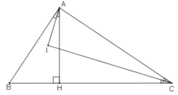
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.
Đúng 1
Bình luận (1)
Cho tam giác ABc, có A=90o. Tia phân giác BE của góc ABC( E thuộc AC). Trên BC lấy sao cho BM=BA.
a)CM: tam giác BEA= tam giác BEM
b) CM: EM vuông góc với BC
c) So sánh góc ABC và góc MEC
a, Xét tam giác BEA và tam giác BEM có;
BA=BM(gt)
B1=B2(BE là tia p/g của góc ABC)
BE: chung
suy ra tg BEA=tg BEM
b,Có tg BEA = tg BEM (cmt)
suy ra A=M1=90o ( 2 góc t/ứng)
suy ra EM vuông góc với BC tại M
=))) c, tự làm nhé
Đúng 0
Bình luận (0)