1.Cho tam giác ABC. Vẽ bên ngoài tam giác ABC các tam giác đều ABD và BCE. Gọi M, N, P là trung điểm AC, BD, BE. Chứng minh tam giác MNP đều
2.Cho tam giác ABC có I là giao điểm các tia phân giác các góc B và C. Gọi M là trung điểm của BC. Biết góc BIM=90 độ và BI =2IM
a)Tính góc BAC
b)Vẽ IH vuông góc với AC( H thuộc AC). Chứng minh BA = 3IH
câu a bài 2 nhá
a) Gọi D là trung điểm BI => góc IDM = 45 độ
DM // IC ( đường trung bình )
=> góc BIC = 135 độ
=> 180 -1/2( góc B + góc C ) =135 độ
=> góc B + góc C = 90 độ
=> góc A = 90 độ
Cho hình vẽ như bên dưới:
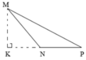
Trong tam giác MNP, MK là chiều cao tương ứng với:
A. Cạnh MN
B. Cạnh NP
C. Cạnh MP
D. Cạnh KN
Hình tam giác MNP có MK vuông góc với NP, do đó MK là chiều cao tương ứng với cạnh đáy NP.
Đáp án B
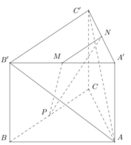
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có A B = 2 3 , A A ' = 2 . Gọi M, N, P lần lượt là trung điểm của các cạnh A ' B ' , A ' C ' và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng ( A B ' C ' ) v à ( M N P ) bằng
A. 6 13 65
B. 13 65
C. 17 13 65
D. 18 13 65
Đáp án B
Gọi L là điểm thỏa mãn A P ¯ = 3 P L ¯ và Q là trung điểm B ' C ' thì cosin cần tìm là
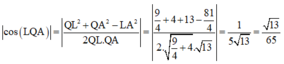
Cho hình lăng trụ tam giác đều ABC.A'B'C' có A B = 2 3 , A A ' = 2 . Gọi M, N, P lần lượt là trung điểm của các cạnh A'B',A'C' và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng ( AB'C' ) và ( MNP ) bằng
A. 6 13 65
B. 13 65
C. 17 13 65
D. 18 13 65
Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B
Cho hình tam giác MNP,trên NP lấy điểm K sao cho NK=1/2 KP nối MK(như hình vẽ).Tính diện tích hình tam giác MNP,biết diện tích hình tam giác MNK bằng 54cm2
Cho hình tam giác MNP,trên NP lấy điểm K sao cho NK=1/2 KP nối MK(như hình vẽ).Tính diện tích hình tam giác MNP,biết diện tích hình tam giác MNK bằng 54cm2
cho tam giác MNP. Trên cạnh MN lấy điểm E sao cho ME=3 x EN. Tính diện tích tam giác MNP biết diện tích tam giác ENP là 27,5 cm2. ( vẽ hình vào vở)
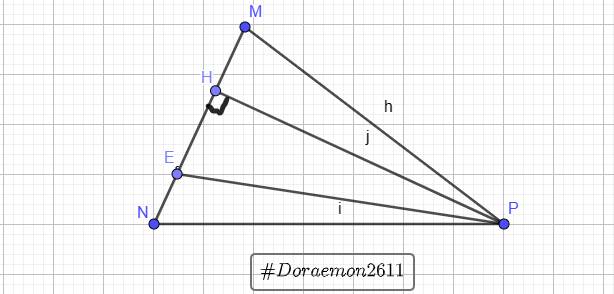
Gọi `PH \bot MN`
Diện tích `\triangle EMP` có `PH` là đường cao
`=>S_[\triangle EMP]=1/2 xxPHxxEN`
`=>1/2 xxPHxxEN=27,5`
`=>PHxxEN=55`
Mà `EN=1/4 MN`
`=>PHxx1/4 MN=55`
`=>PHxxMN=220`
Diện tích `\triangle MNP` có `PH` là đường cao
`=>S_[\triangle MNP]=1/2 xxPHxxMN=1/2 xx220=110(cm^2)`
Cho hình tam giác MNP , trên NP lấy điểm K sao cho NK = 1/2 KP , nối MK (như hình vẽ) . Tính diện tích tam giác MNP , biết diện tích tam giác MNK bằng 54m2
Xét tam giác MNP và tam giác MNK có chung chiều cao hạ từ M xuống NP,đáy NK=12=12 NP hay đáy NP gấp đôi đáy NK nên diện tích tam giác MNP gấp 2 lần diện tích tam giác MNK.
Diện tích tam giác MNP là:
54×2=10854×2=108 (cm2cm2 )
ĐS: 108108 cm2
Cho tam giác MNP cân tại M, đường cao MQ .Gọi H là trung điểm của MN, R là điểm đối xứng của Q qua H .
a, Chứng minh rằng tứ giác MPQH là hình thang
b, Tứ giác MQNR là hình gì ? Vì sao ?
c,Nếu tam giác MNP là tam giác đều thì tứ giác MPQH là hình gì ? Vì sao?
Nhớ vẽ hình nhé !
