Cho góc xOy=900 ; phân giác Oz. Lấy điểm M thuộc tia Oz.
Kẻ MA ⊥ Ox; MB ⊥ Oy (A ∈ Ox; B ∈ Oy). Lấy K thuộc đoạn MA (K khác A, M).
Lấy H thuộc đoạn MB sao cho góc AKO=góc OKH
Khi đó KOH=

Những câu hỏi liên quan
Cho hai góc kề bù góc xOy và góc yOz .Om là phân giác góc xOy và On là phân giác yOz . Chứng minh: góc mOn =900
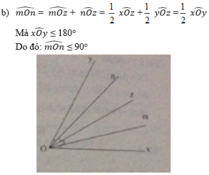
góc mOn=góc mOy+góc nOy
=1/2*(góc xOy+góc yOz)=90 độ
Đúng 0
Bình luận (0)
1) Vẽ góc xOy = 900 ; góc xOz = 450 .
a/ Trên hình vẽ có bao nhiêu góc? Viết tên các góc đó.
b/ Trên hình vẽ có góc nào là góc vuông? Góc nhọn? Góc tù
c/ Tính số đo góc yOz.1) Vẽ góc xOy = 900 ; góc xOz = 450 .
chỉ mình với ạ !!!
a: góc xOz; góc yOz; góc xOy
b: vuông: góc xOy
nhọn: góc xOz; góc yOz
c: góc yOz=45 độ
Đúng 0
Bình luận (0)
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Góc xOy = 900. Chứng minh góc x’Oy, xOy’ và x’Oy’ vuông
mọi người làm nhanh giúp mk với ạ , mk đang vội
Ta có: \(\widehat{xOy}=90^0\)
nên \(xx'\perp yy'\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{xOy'}=90^0\\\widehat{x'Oy'}=90^0\\\widehat{x'Oy}=90^0\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho góc xOy bằng 1200, vẽ tia Oz nằm giữa hai tia Ox và Oy sao cho góc xOz bằng 900.|
vẽ hình cho mình nhé
chỉ là hình minh họa thôi nha bạn, bạn tự lấy thức đo độ vẽ lại
Đúng 0
Bình luận (1)
Bài 4: Vẽ hình theo cách diễn đạt sau :a ; Cho góc xoy 900 . Trên tia phân giác 0t của góc xoy lấy điểm M . Qua M vẽ đường thẳng vuông góc với 0x tại P; Qua M vẽ đường thẳng vuông góc với 0y tại Q;b ; Cho góc xoy tù. Từ điểm M nằm trên nửa mặt phẳng bờ chứa tia 0y không chứa 0x vẽ hai đường thẳng qua M vuông góc với đường thẳng chứa tia 0x tại P và vuông góc với đường thẳng chứa tia 0y tại Q. Từ Q vẽ đường thẳng vuông góc với OM tại H , Từ P vẽ đường thẳng vuông góc với OM tại K
Đọc tiếp
Bài 4: Vẽ hình theo cách diễn đạt sau :
a ; Cho góc xoy = 900 . Trên tia phân giác 0t của góc xoy lấy điểm M . Qua M vẽ đường thẳng vuông góc với 0x tại P; Qua M vẽ đường thẳng vuông góc với 0y tại Q;
b ; Cho góc xoy tù. Từ điểm M nằm trên nửa mặt phẳng bờ chứa tia 0y không chứa 0x vẽ hai đường thẳng qua M vuông góc với đường thẳng chứa tia 0x tại P và vuông góc với đường thẳng chứa tia 0y tại Q. Từ Q vẽ đường thẳng vuông góc với OM tại H , Từ P vẽ đường thẳng vuông góc với OM tại K
b)Cho (xOy, tia Oz nằm giữa hai tia Ox, Oy. Gọi Om, On lần lượt là tia phân giác của các góc (xOz, (xOy. Chứng minh rằng (mOn ≤ 90 0
Bài 1. Cho góc xOy = 900 . A là điểm trên tia Ox không trùng với góc O. Vẽ đường thẳng t vuông góc với Ox tại A. Chứng tỏ rằng t // O
ài 84: Cho xOy 900 . Lấy A trên tia phân giác của xOy , M là trung điểm của OA. Từ M kẻ
đường thẳng vuông góc với OA, cắt Oy ở B.
1) Chứng minh AB // Ox
2) Tính số đo xOy để OBA 100
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 900 . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 300 . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
a ) Ta có : xOy + yOx ' = 180 ( kề bù )
\(\Rightarrow\) 90 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 90 = 90
Lại có : xOy + y ' Ox = 180 ( kề bù )
\(\Rightarrow\) 90 + y ' Ox = 180
\(\Rightarrow\) y ' Ox = 180 - 90 = 90
Ta thấy : xOy ' + y ' Ox ' = 180 ( kề bù )
\(\Rightarrow\) 90 + y ' Ox ' = 180
\(\Rightarrow\) y ' Ox ' = 180 - 90 = 90
b ) Ta có : xOy + yOx ' = 180 ( kề bù )
\(\Rightarrow\) 30 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 30 = 150
Lại có : xOy + yOx '= 180 ( kề bù )
\(\Rightarrow\) 30 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 30 = 150
Ta thấy : x ' Oy + y ' Ox ' = 180 ( kề bù )
\(\Rightarrow\) 150 + y ' Ox ' = 180
⇒ y ' Ox ' = 180 - 150 = 3
Bài làm lại :
a ) \(\widehat{xOy}+\widehat{y'Oy}=180^o\)( KB )
\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-90^o=90^o\)( Đối đỉnh )
Vậy \(\widehat{xOy}'=\widehat{y'Ox}=90^o\)( Đối đỉnh )
b ) \(\widehat{xOy}+\widehat{x'Oy}=180^o\)( KB )
\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-30^o=150^o\)
Vậy \(\widehat{xOy}=\widehat{x'Oy'}=30^o\)( Đối đỉnh )
\(\widehat{yOx'}=\widehat{y'Ox}=150^o\)( Đối đỉnh )
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 900.
Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 300.
Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
Bài giải
a) yOx' ; x'Oy' ; y'Ox đều bằng 90 độ
b) yOx' bằng 150 độ ; x'Oy' bằng 30 độ ; y'Ox bằng 150 độ
Học tốt !