Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với ( ABCD), SA = AB= a; AD= 3a. M là trung điểm của BC. Tính cos(( SDM); ( ABCD))

Những câu hỏi liên quan
Cho hình chóp S. ABCD đáy ABCD là hình chữ nhật, ABa, AD2a. Cạnh bên SA vuông góc với đáy (ABCD), SA2a. Tính tan của góc giữa hai mặt phẳng (SBD) và (ABCD) A.
1
5
B.
2
5
C.
5
D.
5
2
Đọc tiếp
Cho hình chóp S. ABCD đáy ABCD là hình chữ nhật, AB=a, AD=2a. Cạnh bên SA vuông góc với đáy (ABCD), SA=2a. Tính tan của góc giữa hai mặt phẳng (SBD) và (ABCD)
A. 1 5
B. 2 5
C. 5
D. 5 2
Cho hình chóp S. ABCD đáy là hình chữ nhật. Biết SA AB a, AD 2a, SA vuông góc (ABCD). Tính bán kính mặt cầu ngoại tiếp hình chóp S. ABCD. A.
2
a
39
13
B.
a
3
2
C.
3
a
3...
Đọc tiếp
Cho hình chóp S. ABCD đáy là hình chữ nhật. Biết SA =AB = a, AD =2a, SA vuông góc (ABCD). Tính bán kính mặt cầu ngoại tiếp hình chóp S. ABCD.
A. 2 a 39 13
B. a 3 2
C. 3 a 3 4
D. a 6 2
Cho hình chóp S. ABCD có SA=a, SA vuông góc với đáy, đáy là hình chữ nhật có AB=a, AD=a^2. Tính góc giữa SC với mặt đáy
Xem chi tiết
hình bạn tự vẽ t chỉ gợi ý cách làm chứ t làm biếng quá :<
góc giữa SC và đáy chính là góc giữa SC và hình chiều của nó lên mặt đáy là AC thực chất ta đi tìm góc giữa SC và AC
hoàn toàn tính đc cạnh AC vì tam giác BAC vuông tại B có AB và BC lần lượn là cạnh góc vuông có độ dài a và a^2
tính đc AC nhìn vào tam giác vuông SAC ta sẽ dùng cos (SC,AC) = AC/SC
:D bài toán khá là đơn giản good luck
Đúng 1
Bình luận (2)
Cho khối chóp S. ABCD , có SA vuông góc với mặt đáy ABCD , SA = x. Mặt đáy là hình chữ nhật ABCD có cạnh là 4x. và 3x . Tính khối chóp S. ABCD.
\(V=\dfrac{1}{3}SA.AB.AD=\dfrac{1}{3}.x.4x.3x=4x^3\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB a, AD 2a, SA a. Tính thể tích khối chóp S.ABCD. A. 2a3 B. a3 C. a3/3 D. 2a3/3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a, SA =a. Tính thể tích khối chóp S.ABCD.
A. 2a3
B. a3
C. a3/3
D. 2a3/3
Đáp án D
Diện tích hình chữ nhật ABCD là S = 2a2, chiều cao SA =a.
Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a , SA=3a và SA vuông góc với (ABCD). Tính góc giữa SD và mặt phẳng ABCD
(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=3/2
=>góc SDA=56 độ
Đúng 0
Bình luận (0)
#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, ABa, BC a
3
, SAa và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
Đọc tiếp
#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, AB=a, BC = a 3 , SA=a và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
![]()
![]()
![]()
![]()
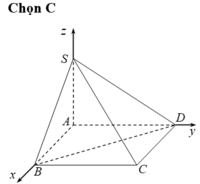
Đặt hệ trục tọa độ Oxyz như hình vẽ.
Khi đó, ta có A (0;0;0), B (a;0;0), D (0; a√3 ; 0), S (0;0;a).
Ta có ![]() , nên đường thẳng BD có vectơ chỉ phương là
, nên đường thẳng BD có vectơ chỉ phương là ![]() .
.
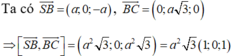
Như vậy, mặt phẳng (SBC) có vectơ pháp tuyến là ![]()
Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì
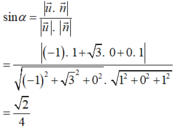
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật,
AD
a
,
AB
2
a
,
cạnh bên
SA
a
3
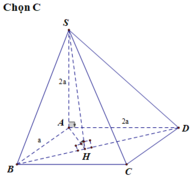
và vuông góc với mặt phẳng đáy (ABCD). Gọi M là trung điểm AB Tính bán kính hình cầu ngoại tiếp hình chóp S.AMD A.
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, AD = a , AB = 2 a , cạnh bên SA = a 3 và vuông góc với mặt phẳng đáy (ABCD). Gọi M là trung điểm AB Tính bán kính hình cầu ngoại tiếp hình chóp S.AMD
A. a 5 4
B. a 3 2
C. a 5 2
D. a 2 2
cho hình chóp s abcd có đáy abcd là hình chữ nhật AB=3a bc=4a sa=5a và SA vuông góc với mặt phẳng ABCD. Tính theo a khoảng cách từ điểm C đến mặt phẳng SBD
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
A
B
2
a
,
B
C
a
,
S
A
a
3
và SA vuông góc với mặt đáy (ABCD). Thể tích V của khối chóp S.ABCD bằng A.
V
2
a
3
3
.
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = 2 a , B C = a , S A = a 3 và SA vuông góc với mặt đáy (ABCD). Thể tích V của khối chóp S.ABCD bằng
A. V = 2 a 3 3 .
B. V = 2 a 3 3 3 .
C. V = a 3 3 .
D. V = a 3 3 3 .
Đáp án B
Do S A ⊥ A B C D
⇒ V S A B C D = 1 3 S A . d t A B C D = 1 3 S A . A B . B C = 1 3 a 3 .2 a . a = 2 a 3 3 3
Đúng 0
Bình luận (0)