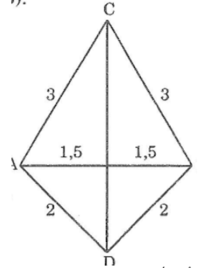
Cho hai tam giác ABC và ABD có AB = BC = CA = 3cm; AD = BD = 2cm. (C và D nằm khác phía đối với AB) Chứng minh rằng : \(\widehat{CAD}\)= \(\widehat{CBD}\)

Những câu hỏi liên quan
Cho hai tam giác ABC và ABD có AB = BC = CA = 3cm, AD = BD = 2cm (C và D nằm khác phía đối với AB). Chứng minh rằng: ∠(CAD) =∠(CBD)
Xét ΔCAD và ΔCBD, ta có:
AC = BC (= 3 cm)
AD = BD (= 2 cm)
CD cạnh chung
Suy ra: ΔCAD= ΔCBD(c.c.c)
Vậy ∠(CAD) =∠(CBD) ̂(hai góc tương ứng)
Đúng 0
Bình luận (0)
Cho tam giác ABC và ABD có AB=BC=CA=3cm, AD=BD=2cm (C và D nằm khác phía với AB) Chứng minh góc CAD = góc CBD.
xét 2 tam giác ACD và BCD có AD=BD=2cm, AC=BC=3cm, CD chung
=> tg ACD= tg BCD (c.c.c) =>góc CAD= góc CBD
Đúng 1
Bình luận (1)
1, Cho tam giác ABC và tam giác ABD có AB=BC=CA=3cm, AD=BD=2cm (C và D nằm khác phía đối với AB)
a) Ch/minh rằng tam giác CAD=Tam giác CBD
b) Ch/minh rằng CAD=CBD ( mik cần vẽ hình và giải đáp ạ ) giúp mik với ^^
a,Xét tam giácCAD và tam giác CBD có:
CD:cạnh chumg
CA=CB
AD=BD
----->Tam giác CAD=tam giác CBD(c.c.c)
Vậy....
b,Có tam giác CAD=tam giác CBD(cmt)
-->Góc CAD=góc CBD(cặp góc tương ứng )
Vậy...
Đúng 0
Bình luận (3)
cho tam giác abc có ab=5cm,bc=4cm,ac=3cm
a,tính số đo góc ACB
b,trên tia đối của tia CA lấy điểm D sao cho CD=3cm. Chứng minh tam giác ABD cân
a, Có AB ^2 = 5^2=25
Có BC^2 +AC ^2= 4^2 +3^2=16+9=25
\(\Rightarrow\)AB^2 = AC^ 2+ BC^2 (=25)
\(\Rightarrow\)Tam giác ABC là tam giác vuông tại C ( Định lý pytago đảo)
\(\Rightarrow\)Góc ACB = 90 độ
b, Có góc BCD + góc ACB = 180 độ( 2 góc kề bù)
góc BCD + 90 độ = 180 độ
góc BCD = 90 độ
Xét tam giác ABC và BDC , có:
AC=CD ( vì cùng = 3cm)
góc ACB = góc BCD ( vì cùng = 90 độ)
BC là cạnh chung
\(\Rightarrow\)Tam giác ABC= Tam giác BCD (c.g.c)
\(\Rightarrow\) AB = BD (2 cạnh tương ứng)
Xét tam giác ABD, có:
AB = BD (chứng minh trên)
\(\Rightarrow\)Tam giác ABD cân tại B
Cho hai tam giác ABC và tam giác ABD có AB=BC=CA=3 cm.AD=BD=2 cm (C và D nằm khác phí với AB).Chứng minh CAD=CBD
Vì tam giác ABC có AB=BC=AC
=> tam giác ABC đều
=> ABC=ACB=BAC
Tam giác BAD có
DA=DB
=> tam giác BDA cân tại D
=> DAB=DBA
Lại có
CAD=CAB+BAD
CBD=CBA+ABD
Vì BAC=ABC, BAD=ABD
=> CAD=CBD
=> DPCM
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và ABD có AB = BC = CA = 3cm; AD = BD = 2cm. (C và D nằm khác phía đối với AB)
Chứng minh rằng :
\(\widehat{CAD}=\widehat{CBD}\)
Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm.
a) Tính độ dài cạnh BC
b) Vẽ đường phân giác BD của tam giác ABC (D thuộc AC). Vẽ DE vuông góc BC tại E. Chứng minh tam giác ABD = tam giác EBD và Góc BED = 90 độ
c)Hai đường thẳng AB và ĐE cắt nhau tại F. Chứng minh BI là đường trung trực của EF
d) Gọi I là giao điểm của BD và FC. Chứng minh BI là đường trung trực của EF
Cho tam giác ABC và tam giác ABD
AB=BC=CA= 3cm
AD=BD= 2cm (C và D khác phía đối với AB )
Chứng minh góc CAD = góc CBD
Trình bày rõ ràng nhá
Cho tam giác ABC và tam giác ABD
AB=BC=CA= 3cm
AD=BD= 2cm (C và D khác phía đối với AB )
Chứng minh góc CAD = góc CBD
Trình bày rõ ràng nhá
Cho tam giác ABC và tam giác ABD
AB=BC=CA= 3cm
AD=BD= 2cm (C và D khác phía đối với AB )
Chứng minh góc CAD = góc CBD
Trình bày rõ ràng nhá



















