Cho tam giác ABC vuông tại A có AB = 21cm; AC = 72cm và AH là đường cao.
a) Tính các tỉ số lượng giác của góc BAH và số đo của nó.
b) Suy ra các tỉ số lượng giác của góc CAH.
cho tam giác abc vuông tại a có ab=21cm, bc=35cm. a)giải tam giác vuông abc .b)tính độ dài phân giác ad và đường cao ah
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{35^2-21^2}=28\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
=>\(\widehat{B}\simeq53^0\)
=>\(\widehat{C}\simeq37^0\)
b: Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot sin45=\dfrac{2\cdot21\cdot28}{21+28}\cdot\dfrac{\sqrt{2}}{2}\simeq16,97\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot35=21\cdot28\)
=>\(AH=16.8\left(cm\right)\)
1, Tam giác ABC vuông tại A, kẻ đường cao AH
a.Tính AB, AC,BC, HC nếu AH= 6cm, BH= 4,5cm
b.Biết AB= 6cm, HB- 3cm. Tính AH, AC,CH
5, Cho tam giác ABC vuông tại A có AB=21cm, góc C= 40 độ
a.Tính AC
b,Tính BC
Bài 5:
a) Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(=21\cdot\cot40^0\)
\(\simeq25,03\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+25,03^2=1067,5009\)
hay \(BC\simeq32,67\left(cm\right)\)
cho tam giác ABC vuông tại A có AB=21cm,C=40 độ.Hãy tính độ dài :AC,BC,phân giác AD
Xét ΔABC vuông tại A có
tan C=AB/AC
=>21/AC=tan 40
=>\(AC\simeq25,03\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}\simeq32,67\left(cm\right)\)
cho tam giác ABC vuông tại B, AB=21cm, BC=18cm. Giải tam giác ABC
Cho tam giác ABC có AB=21cm,AC=29cm
A)chứng minh tam giác ABC vuông
B)Trên tia BA lấy D sao cho BD=BC.Vẽ DE vuông góc với BC tại E.Chứng minh:tam giác BAC=tam giác BED
ý a) hình như thiếu gt mình không làm được
b) theo gt ta có : DE vuông góc với BC
=> tam giác BED là tam giác vuông
Xét tam giác vuông ABC và tam giác vuông BED có :
+ góc B chung
+ BD = BC
=> tam giác vuông ABC và tam giác vuông BED ( cạnh huyền + góc nhọn )
Cho tam giác ABC vuông tại A có AB=21cm , AC=28cm.Đường phân giác của góc A cắt BC tại D.Đường thẳng qua DE // AB(E thuộc AC)
a,Tính BD,DC,DE
b, Tính diện tích tam giác ABD và diện tích tam giác ACD.
Cho tam giác ABC vuông tại A, có AB = 21cm, AC = 28cm. Kẻ phân giác trong AD của B A C ^ (với D ∈ B C ). Tính BD, CD
Cho tam giác ABC vuông tại A có AB=21cm, AC=28cm, đường phân giác AD.
Tính độ dài cạnh AD
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 ° . Hãy tính các độ dài: Phân giác BD
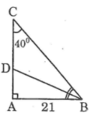
Cho tam giác ABC vuông tại A,AB=21cm,góc C=40 độ .Tính
a,AC,BC b,Phân giác BD
a) Ta có:
\(sin40=\dfrac{AB}{BC}=\dfrac{21}{BC}\)\(\Rightarrow BC=\dfrac{21}{sin40}\simeq33cm\)
\(cos40=\dfrac{AC}{BC}\Rightarrow AC=cos40.33\simeq25cm\)
b) \(sinB=\dfrac{AC}{BC}=\dfrac{25}{33}\Rightarrow\widehat{B}\simeq49^o\)
\(BD=\dfrac{2.BC.AB.cos24,5}{BC+AB}\simeq12cm\)
\(Taco.\dfrac{BC}{sinA}=\dfrac{AB}{SinC}\Rightarrow BC=32,67cm=>AC=\sqrt{32,67^2-21^2}=25cm\)
Taco ^B=90-40=30 do
\(BD=\dfrac{2.21.32,67}{21+32,67}.CosB:2=24,69cm\)