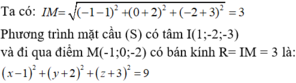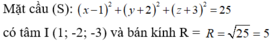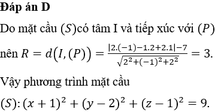Trong không gian Oxyz, viết phương trình của mặt cầu (S) có tâm I(−2; 0; 5) và bán kính R = 2.

Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là: A.
(
x
-
1
)
2
+
(
y
+
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là:
A. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 3
B. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9
C. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 3
D. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 9
Trong không gian tọa độ Oxyz cho mặt cầu (S) có tâm I(1;-2;3) và đường thẳng d có phương trình
x
1
+
2
t
y
-
1
-
t...
Đọc tiếp
Trong không gian tọa độ Oxyz cho mặt cầu (S) có tâm I(1;-2;3) và đường thẳng d có phương trình x = 1 + 2 t y = - 1 - t z = 1 + 2 t . Biết rằng mặt cầu (S) tiếp xúc với đường thẳng d. Viết phương trình mặt cầu (S).
![]()
![]()
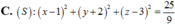
![]()
Trong không gian Oxyz, cho mặt phẳng
α
: 4x-3y+2z+280 và điểm I(0;1;2). Viết phương trình của mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng
α
.
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng α : 4x-3y+2z+28=0 và điểm I(0;1;2). Viết phương trình của mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng α .
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S). A.
x
2
+
y
2
+
z
-
3
2
9
B.
x
2
+
y
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
A. x 2 + y 2 + z - 3 2 = 9
B. x 2 + y 2 + z + 3 2 = 9
C. x - 3 2 + y 2 + z 2 = 3
D. x - 3 2 + y 2 + z 2 = 9
Chọn D.
Phương pháp: Tìm tâm và bán kính mặt cầu.

Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 25
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -3); R = 25
B. I(-1; 2; 3); R = 5
C. I(-1; 2; 3); R = 25
D. I(1; -2; -3); R = 5
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(1;-1;1) và mặt phẳng (P): 2x - y + 2z + 1 0. Biết (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S). A.
(
x
-
1
)
2
+
(
y
+
1
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(1;-1;1) và mặt phẳng (P): 2x - y + 2z + 1 = 0. Biết (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S).
A. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 13
B. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 169
C. ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 169
D. ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 169
Trong không gian Oxyz, cho điểm I(3;-1;4) và mặt cầu
(
S
1
)
:
(
x
-
1
)
2
+
y
2
+
(
z
-
2
)
2
1
. Phươn...
Đọc tiếp
Trong không gian Oxyz, cho điểm I(3;-1;4) và mặt cầu ( S 1 ) : ( x - 1 ) 2 + y 2 + ( z - 2 ) 2 = 1 . Phương trình của mặt cầu (S) có tâm Ivà tiếp xúc ngoài với mặt cầu ( S 1 ) là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I (0; -2; 1) và mặt phẳng (P): x + 2y - 2z + 3 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích là 2π. Viết phương trình mặt cầu (S). A.
(
S
)
:
x
2
+
(
y
+...
Đọc tiếp
Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I (0; -2; 1) và mặt phẳng (P): x + 2y - 2z + 3 = 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích là 2π. Viết phương trình mặt cầu (S).
A. ( S ) : x 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 3
B. ( S ) : x 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 1
C . ( S ) : x 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 3
D. ( S ) : x 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 2
Chọn C
Ta có h = d(I, (P)) = 1
Gọi (C) là đường tròn giao tuyến có bán kính r.
Vì S = r2.π = 2π <=> r = √2
Mà R2 = r2 + h2 = 3 => R = √3
Vậy phương trình mặt cầu tâm i (0; -2; 1) và bán kính R = √3
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 1) và mặt phẳng (P): 2x - y + 2z - 7 0. Viết phương trình mặt cầu (S) có tâm I và tiếp xúc với (P).
A
.
(
S
)
:
(
x
+
1
)
2
+
(
y
-
2
)
2
+
(
z
-
1
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 1) và mặt phẳng (P): 2x - y + 2z - 7 = 0. Viết phương trình mặt cầu (S) có tâm I và tiếp xúc với (P).
A . ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 1 ) 2 = 3
B . ( S ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 9
C . ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 3
D . ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 1 ) 2 = 9