a) cho d: 2x-3y+12=0. Tìm ảnh của d qua phép tịnh tiến theo v = (4; -3) b) cho d : 2x+y-4=0 và A (3;1) ;B (-1;8) . Tìm ảnh d' của d qua phép tịnh tiến theo AB->

Những câu hỏi liên quan
Tìm ảnh của đường thẳng
d
:
2
x
+
3
y
−
2
0
qua phép tịnh tiến theo vecto
v
→
2
;
3
là A.
2
x
+
3
y
+
15
0
B.
2
x
−
3...
Đọc tiếp
Tìm ảnh của đường thẳng d : 2 x + 3 y − 2 = 0 qua phép tịnh tiến theo vecto v → = 2 ; 3 là
A. 2 x + 3 y + 15 = 0
B. 2 x − 3 y + 15 = 0
C. 2 x − 3 y − 15 = 0
D. 2 x + 3 y − 15 = 0
Trong mặt phẳng tọa độ Oxy cho vectơ
v
→
-
1
;
2
,
A
3
;
5
,
B
-
1
;
1
và đường thẳng d có phương trình
x
–
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
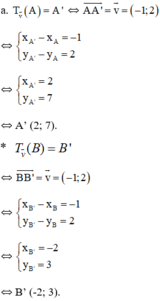
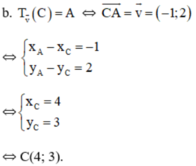
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
Đúng 0
Bình luận (0)
7. Tìm ảnh d’ của đường thẳng d: 2x – y – 1 = 0 qua phép tịnh tiến theo vector v=(2;-1)
Do d' là ảnh của d qua phép tịnh tiến \(\Rightarrow\) d' cùng phương d
Phương trình d' có dạng: \(2x-y+c=0\)
Lấy \(A\left(0;-1\right)\) là 1 điểm thuộc d
\(T_{\overrightarrow{v}}\left(A\right)=A'\Rightarrow\left\{{}\begin{matrix}x'=0+2=2\\y'=-1+\left(-1\right)=-2\end{matrix}\right.\)
\(\Rightarrow A'\left(2;-2\right)\)
Thế vào pt d':
\(2.2-\left(-2\right)+c=0\Rightarrow c=-6\)
Vậy pt d' là: \(2x-y-6=0\)
Đúng 0
Bình luận (0)
Trong mp Oxy cho điểm A(1,2),đường thẳng d co pt:2x-3y+10 và véc tơv(-3,1)a)Tìm ảnh của A,(d) qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 độ và phép tịnh tiến theo vb) tìm điểm M sao cho A là ảnh của M qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay- 90 độ và phép tịnh tiến theo vc) tìm điểm d’ sao cho d là ảnh của d’ qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay- 90 độ và phép tịnh tiến theo v
Đọc tiếp
Trong mp Oxy cho điểm A(1,2),đường thẳng d co pt:2x-3y+1=0 và véc tơ
v=(-3,1)
a)Tìm ảnh của A,(d) qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 độ và phép tịnh tiến theo v
b) tìm điểm M sao cho A là ảnh của M qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay- 90 độ và phép tịnh tiến theo v
c) tìm điểm d’ sao cho d là ảnh của d’ qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay- 90 độ và phép tịnh tiến theo v
Cho vecto v (-2;1); d: 2x-3y+30 ; d1: 2x-3y-501) Viết phương trình d’ Tv(d)2) Tìm toạ độ vecto w có phương vuông góc với d để d1 Tw(d)Cho (d): 3x-y-90. Tìm phép tịnh tiến theo phương song song với trục Ox biến d thành d’ đi qua gốc toạ độ. Hãy viết phương trình d’.Trong hệ trục toạ độ Oxy, cho parabol (P): y ax^2Gọi T là phép tịnh tiến theo vecto u(m;n) và (P’) là ảnh của (P) qua phép tịnh tiến đó. Hãy viết phương trình của (P’).Cho đường thẳng Delta: 6x+2y-10. Tìm vecto u nevecto 0 để DeltaTu(D...
Đọc tiếp
Cho vecto v= (-2;1); d: 2x-3y+3=0 ; d1: 2x-3y-5=0
1) Viết phương trình d’= Tv(d)
2) Tìm toạ độ vecto w có phương vuông góc với d để d1= Tw(d)
Cho (d): 3x-y-9=0. Tìm phép tịnh tiến theo phương song song với trục Ox biến d thành d’ đi qua gốc toạ độ. Hãy viết phương trình d’.
Trong hệ trục toạ độ Oxy, cho parabol (P): y= \(ax^2\)Gọi T là phép tịnh tiến theo vecto u=(m;n) và (P’) là ảnh của (P) qua phép tịnh tiến đó. Hãy viết phương trình của (P’).
Cho đường thẳng \(\Delta\): 6x+2y-1=0. Tìm vecto u \(\ne\)vecto 0 để \(\Delta=\)Tu(\(\Delta\))
Trong mp Oxy cho \(\overrightarrow{v}\left(1;2\right)\), d: x - 3y + 6 = 0. Tìm ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo \(\overrightarrow{v}\) và phép quay tâm O góc \(\dfrac{-\pi}{2}\)
Cho mặt phẳng tọa độ Oxy cho 4 điểm A(-1;2) B(3;-4) C(0;-5) D(-6;7)
a) tìm ảnh A, B, C, D qua phép tịnh tiến thao vecto v=(-2;1)
b) Tìm E, F sao cho TAB(E)=C ; TDC (F)=D
c) gọi I là trung điểm của AB. Tìm G sao cho I là ảnh của G qua phép tịnh tiến theo vecto DC
Trong mp Oxy cho đường thẳng d: x+3y+1=0 .Viết phương trình đường thẳng là ảnh của d qua phép tịnh tiến theo véc tơ v= (3 ;-2)
Giải giúp mk vs ạ
Gọi \(M\left(x;y\right)\) là 1 điểm bất kì thuộc d \(\Rightarrow x+3y+1=0\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép tịnh tiến nói trên thì \(M'\in d'\) với d' là ảnh của d
\(\left\{{}\begin{matrix}x'=x+3\\y'=y-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'-3\\y=y'+2\end{matrix}\right.\)
Thế vào (1):
\(x'-3+3\left(y'+2\right)+1=0\)
\(\Leftrightarrow x'+3y'+4=0\)
Vậy pt ảnh có dạng \(x+3y+4=0\)
Đúng 1
Bình luận (0)
Viết pt đường thẳng d’ là ảnh của d: 2x-5y=1=0 qua phép tịnh tiến theo v ( -5;3)
mog mn giúp đỡ












