Cho phương trình a x 2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; △ ' = b ' 2 - ac. Nếu △ ' = 0 thì:
A. Phương trình có hai nghiệm phân biệt
C. Phương trình có nghiệm kép x 1 = x 2 = - b ' a
D. Phương trình có nghiệm kép x 1 = x 2 = - b ' 2 a
Những câu hỏi liên quan
Cho phương trình a
x
2
+ bx + c 0 (a
≠
0) có biệt thức b 2b;
△
b
2
- ac. Phương trình đã cho có hai nghiệm phân biệt khi: A.
△
0 B.
△
0 C.
△
≥
0 D.
△
≤
0
Đọc tiếp
Cho phương trình a x 2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; △ ' = b ' 2 - ac. Phương trình đã cho có hai nghiệm phân biệt khi:
A. △ ' > 0
B. △ ' = 0
C. △ ' ≥ 0
D. △ ' ≤ 0
Đáp án A
Xét phương trình bậc hai a x 2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b ' 2 - ac:
• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm
• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép
x
1
=
x
2
= 
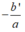
• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt
x
1
,
2
= 
Đúng 0
Bình luận (0)
Cho phương trình a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
b
2
b
’
;
Δ
b
2
−
a
c
Phương trình đã cho có hai nghiệm phân biệt khi? A....
Đọc tiếp
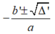
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2 b ’ ; Δ ' = b ' 2 − a c Phương trình đã cho có hai nghiệm phân biệt khi?
A. Δ ' > 0
B. Δ ' = 0
C. Δ ' ≥ 0
D. Δ ' ≤ 0
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
với b = 2b’ và biệt thức Δ ' = b ' 2 − a c
Trường hợp 1: Nếu ∆ < 0 thì phương trình vô nghiệm
Trường hợp 2: Nếu ∆ = 0 thì phương trình có nghiệm kép x1 = x2 = − b ' a
Trường hợp 3: nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt
x1,2 = − b ' ± Δ ' a
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức b 2b;
Δ
b
2
-
a
c
. Phương trình đã cho có hai nghiệm phân biệt khi: A.
△
0 B.
△
0 C.
△
≥
0...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2b'; Δ ' = b ' 2 - a c . Phương trình đã cho có hai nghiệm phân biệt khi:
A. △ ' > 0
B. △ ' = 0
C. △ ' ≥ 0
D. △ ' ≤ 0
Đáp án A
Xét phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2b'; Δ ' = b ' 2 - a c :
• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm
• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép
x
1
=
x
2
= 
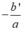
• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt
x
1
,
2
= 
Đúng 0
Bình luận (0)
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
b
2
b
’
;
Δ
b
2
−
a
c
Phương trình đã cho vô nghiệm khi? A.
Δ...
Đọc tiếp
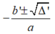
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2 b ’ ; Δ ' = b ' 2 − a c Phương trình đã cho vô nghiệm khi?
A. Δ ' > 0
B. Δ ' = 0
C. Δ ' ≥ 0
D. Δ ' < 0
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
với b = 2b’ và biệt thức Δ ' = b ' 2 − a c
Trường hợp 1: Nếu Δ ' < 0 thì phương trình vô nghiệm
Trường hợp 2: Nếu Δ ' = 0 thì phương trình có nghiệm kép x1 = x2 = − b ' a
Trường hợp 3: nếu Δ ' > 0 thì phương trình có hai nghiệm phân biệt
x1,2 = − b ' ± Δ ' a
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức b 2b;
Δ
b
2
-
a
c
. Nếu
Δ
0
thì: A. Phương trình có hai nghiệm phân biệt B. Phương trình có nghiệm kép ...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2b'; Δ ' = b ' 2 - a c . Nếu Δ ' = 0 thì:
A. Phương trình có hai nghiệm phân biệt
B. Phương trình có nghiệm kép x 1 = x 2 = - b a
C. Phương trình có nghiệm kép x 1 = x 2 = - b ' a
D. Phương trình có nghiệm kép x 1 = x 2 = - b ' 2 a
Đáp án C
Xét phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2b'; Δ ' = b ' 2 - a c :
Nếu Δ' = 0 thì phương trình có nghiệm kép
x
1
=
x
2
= 
Đúng 0
Bình luận (0)
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
b
2
b
’
;
Δ
b
2
−
a
c
nếu
Δ
0
thì? A. Phương trình có...
Đọc tiếp
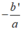
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2 b ’ ; Δ ' = b ' 2 − a c nếu Δ ' = 0 thì?
A. Phương trình có hai nghiệm phân biệt
B. Phương trình có nghiệm kép x 1 = x 2 = b a
C. Phương trình có nghiệm kép x 1 = x 2 = − b a
D. Phương trình có nghiệm kép x 1 = x 2 = − b 2 a
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
có b = 2b’và biệt thức Δ ' = b ' 2 − a c
Nếu Δ ' =0 thì phương trình có nghiệm kép = − b a
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Xét hai câu sau:
P: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\)”.
a) Hãy phát biểu mệnh đề \(P \Rightarrow Q\).
b) Hãy phát biểu mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(P \Rightarrow Q\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\).”
Mệnh đề \(Q \Rightarrow P\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\) thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.”
Đúng 0
Bình luận (0)
Cho a,b,c là 3 số phân biệt sao cho các phương trình: x2+ax+1=0 và x2+bx+c=0 có nghiệm chung. Đồng thời các phương trình x2+x+a=0 và x2+cx+b=0 cũng có nghiệm chung.
Tính giá trị của biểu thức P=a+b+c
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
∆
b
2
–
4
a
c
0
, khi đó, phương trình đã cho: A. Vô nghiệm B. Có nghiệm kép C. Có hai nghiệm phân biệt D. Có 1 nghiệm
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức ∆ = b 2 – 4 a c > 0 , khi đó, phương trình đã cho:
A. Vô nghiệm
B. Có nghiệm kép
C. Có hai nghiệm phân biệt
D. Có 1 nghiệm
Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình
có nghiệm kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình
có hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)