Cho tứ diện ABCD. Các điểm P,Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR=2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Tính tỉ số SA/SD là:
A. 2
B. 1/2
C. 1/3
D. 1
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp
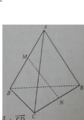
A. GM = GN
B. G M → + G N → = 0 →
C. G A → + G B → + G C → + G D → = 0
D. P G → = 1 / 4 ( P A → + P B → + P C → + P D → ) , với P là điểm bất kì.
Điều kiện GM = GN mới chứng tỏ điểm G nằm trên mặt phẳng trung trực của đoạn thẳng MN.
Đáp án A
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
A. G A → + G B → + G C → + G D → = 0 →
B. 4 P G → = P A → + P B → + P C → + P D → với P là điểm bất kỳ
C. G M = G N
D. G M → + G N → = 0 →
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
![]()
![]() với P là điểm bất kỳ
với P là điểm bất kỳ
![]()
![]()
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A B → + A C → + A D → bằng:
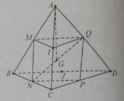
A. 4 A G →
B. 2 A G →
C. A G →
D. 1 / 2 A G →
Ta có N là trung điểm của BC
Suy ra A B → + A C → = 2 A N →
Lại có: A D → = 2 A Q → (Q là trung điểm của AD)
Do đó A B → + A C → + A D → = 2 A N → + 2 A Q → = 2 A N → + A Q → (1)
Tạ lại có G là trọng tâm của tứ diện ABCD nên G là trung điểm của NQ (tính chất trọng tâm của tứ diện) ⇒ A N → + A Q → = 2 A G → (2)
Từ (1) và (2) suy ra A B → + A C → + A D → = 4 A G → .
Đáp án A
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho P A → = m P D → và Q B → = m Q C → , với m khác 1. Vecto M P → bằng:
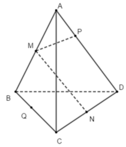
A. M B → − m Q C →
B. M N → − m P D →
C. M A → − m P D →
D. M N → − m Q C →
Có thể loại các phương án A, B và D vì các cặp ba vecto ( M P → , M B → , v à Q C → ) , ( M P → , M N → , P D → ) và ( M P → , M N → v à Q C → ) đều không đồng phẳng.
Phương án C đúng vì : M P → = M A → + A P → = M A → - m P D →
Đáp án C
Cho tứ giác ABCD. Các điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Nối MN, PQ, PQ, QM. Hãy chứng tỏ diện tích tứ giác MNPQ bằng ½ diện tích tứ giác ABCD.
Cho hình thang cân ABCD (AB//CD) và \(\widehat{D}\) = 45 độ. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Tính diện tích các tứ giác ABCD, MNPQ nếu AB = 2cm, CD = 6cm.
b) Tính tỉ số diện tích các tứ giác ABCD, MNPQ nếu các dữ liệu về góc D, cạnh AB, CD không nhất thiết phải như đề cho trên.
Cho hình tứ diện ABCD. Gọi M và N lần lượt là các trung điểm của AB và CD.
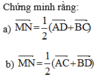
Cho hình tứ diện ABCD, với M,N,P,Q lần lượt là trung điểm của các cạnh AB,BC,CD,DA. Tính diện tích MNPQ biết diện tích của ABCD là 10cm2.