Cho hai góc lượng giác có số đo O x ; O u = 5 π 2 + 2 m π
A.
Cho một góc lượng giác $(O x, O u)$ có số đo $240^{\circ}$ và một góc lượng giác $(O x, O v)$ có số đo $-270^{\circ}$. Tính số đo của các góc lượng giác $(O u, O v)$.
Số đo của các góc lượng giác tia đầu $O u$, tia cuối $O v$ là
\(sđ(O u, O v) = sđ(O x, O v) - sđ(O x, O u)+ k{360}^{\circ}(k \in \mathbb{Z}) \)
\(=-270^{\circ}-240^{\circ}+k 360^{\circ}=-510^{\circ}+k 360^{\circ} \)
\( =-150^{\circ}+(k-1) 360^{\circ}=-150^{\circ}+n 360^{\circ} \quad(n=k-1, n \in \mathbb{Z})
\)
Vậy các góc lượng giác $(O u, O v)$ có số đo là $-150^{\circ}+n 360^{\circ} \quad(n \in \mathbb{Z})$.
Cho góc lượng giác ( OA; OB) có số đo bằng π/5. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác ( OA; O B) ?
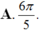
![]()
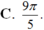
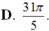
Cho góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{4\pi }}{3}\). Cho góc lượng giác \((O'u',O'v')\) có tia đầu \(O'u' \equiv Ou\), tia cuối \(O'v' \equiv Ov\). Viết công thức biểu thị số đo góc lượng giác \((O'u',O'v')\)
Ta có:
\((O'u',O'v') = (Ou,Ov) + k2\pi \,\, = \, - \frac{{4\pi }}{3}\, + k2\pi \,\,\,\,\,\,\,\,(k \in \mathbb{Z})\)
1)Cho góc xOy có số đo bằng 90 độ .vẽ tia oz nằm giữa hai tia Ox và Oy sao cho góc x o t = 30 độ
A) tính số đo góc yOt
B) hỏi đi ô tô có phải là tia phân giác của góc x O y k ?vì sao?
2) Cho hai góc kề bù x O y và yox', biết góc xOy = góc yOx'. Chứng tỏ góc xOy là góc vuông.
a)góc yot =60 độ b)ko,vì xot và yot ko = nhau
Cho hai góc xOy và yOz là hai góc kề nhau có tổng số đo hai góc là 150o. Biết số đo góc xOy là 90o, góc yOz là 60o. Vẽ Om là tia phân giác của góc xOy, Tia On là tia phân giác của góc yOz. Tính góc mOn.
Cho góc lượng giác (Ou,Ov) có số đo là \( - \frac{{11\pi }}{4}\), góc lượng giác (Ou,Ow) có số đó là \(\frac{{3\pi }}{4}\). Tìm số đo của góc lượng giác (Ov,Ow).
Theo hệ thức Chasles, ta có:
\(\begin{array}{l}(Ov,Ow) = (Ou,Ov) - (Ou,Ow) + k2\pi \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \, - \frac{{11\pi }}{4} - \frac{{3\pi }}{4} + k2\pi = - \frac{7}{2} + k2\pi ,\,\,(k \in \mathbb{Z})\end{array}\)
Cho ▲ABC có góc A = góc B + góc C. Hai đường phân giác của góc B và góc C cắt nhau tại O.
a) Tính số đo góc A.
b) tính số đo góc BOC.
a: góc A=1/2*180=90 độ
b: góc OBC+góc OCB=1/2*90=45 độ
=>góc BOC=135 độ
vẽ hai góc kề bù xOy và yOz, biết số đo góc xOy=50o Vẽ tia Ot là phân giác của xOy. Vẽ Om trong góc yOz sao cho số đo góc tOm=90o
a, Tính số đo góc yOm?
b, Tia Om có là tia phân giác của yOz không? Vì sao?
Trả lời nhanh giúp tớ đi, tớ k cho~