Chứng minh các bất đẳng thức
a+1/a>=17/42a^4+1/1+a^2>=3a^2-1a+4/(a-b)(b-1)^2>=3 (mọi a>b>=0)
Những câu hỏi liên quan
Chứng minh các bất đẳng thức sau
a+1/c (a-b)(b-c)>=4 (mọi a,b,c>0)a+27/2 (a-1)(a+1)^3>=5/2 (mọi a>1)2a+1/(a-b)(b-c)(a+1)^3>=4 (mọi a>b>c>0)Chứng minh các đẳng thức sau:
a
)
2
3
−
6
8
−
2
−
216
3
⋅
1
6
−
1
,
5
b
)...
Đọc tiếp
Chứng minh các đẳng thức sau:
a ) 2 3 − 6 8 − 2 − 216 3 ⋅ 1 6 = − 1 , 5 b ) 14 − 7 1 − 2 + 15 − 5 1 − 3 : 1 7 − 5 = − 2 c ) a b + b a a b : 1 a − b = a − b v ó i a , b d ư ơ n g v à a ≠ b . d ) 1 + a + a a + 1 ⋅ 1 − a − a a − 1 = 1 − a v ó i a ≥ 0 v à a ≠ 1
Biến đổi vế trái:
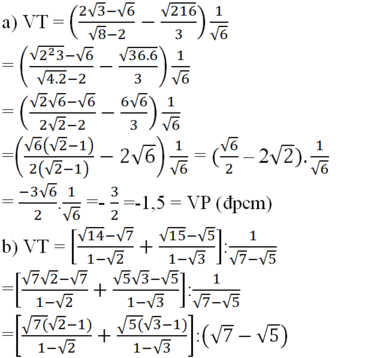
= (-√7 - √5)(√7 - √5)
= -(√7 + √5)(√7 - √5)
= -(7 - 5) = -2 = VP (đpcm)
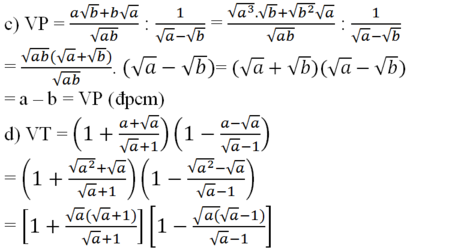
= (1 + √a)(1 - √a)
= 1 - (√a)2 = 1 - a = VP (đpcm)
Đúng 0
Bình luận (0)
chứng minh các bất đẳng thức sau
a/ \(\left(a^2+b^2\right)\left(a^2+1\right)\ge4a^2b\) với mọi a,b
b/ \(\frac{1}{a+3b}+\frac{1}{b+3c}+\frac{1}{c+3a}\ge\frac{1}{a+2b+c}+\frac{1}{b+2c+a}+\frac{1}{c+2a+b}\) với mọi a,b,c>0
a) Áp dụng bất đẳng thức AM-GM :
\(\left(a^2+b^2\right)\left(a^2+1\right)\ge2\sqrt{a^2b^2}.2\sqrt{a^2}\ge2ab.2a=4a^2b\)
b) Áp dụng bất đẳng thức :\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\forall x;y>0\)
\(\frac{1}{a+3b}+\frac{1}{b+2c+a}\ge\frac{4}{a+3b+b+2c+a}=\frac{4}{2a+4b+2c}=\frac{2}{a+2b+c}\)
Tương tự \(\hept{\begin{cases}\frac{1}{b+3c}+\frac{1}{c+2a+b}\ge\frac{2}{b+2c+a}\\\frac{1}{c+3a}+\frac{1}{a+2b+c}\ge\frac{2}{b+2a+c}\end{cases}}\)
Cộng vế với vế ta được : \(VT+VP\ge2VP\Rightarrow VT\ge VP\)(đpcm)
Đúng 0
Bình luận (0)
HÃY CHỨNG MINH BẤT ĐẲNG THỨC SAU :
1 ( a+b)^2 > 4ab với mọi a,b
2 cho a<b . cmr : 3-b/2 < 4- a/2
3 a^2 + b^2 + c^2 > ab + bc + ca với mọi a,b,c
4 a ( a-b) + b ( b-c) + c ( c-a) > 0 với mọi a,b,c
5 a^2 + b^2 + c^2 > 1/3 với a+b+c =1
1. (a+b)^2 ≥ 4ab
<=> a2+2ab+b2≥ 4ab
<=> a2+2ab+b2-4ab≥ 0
<=> a2-2ab+b2≥ 0
<=> (a-b)^2 ≥ 0 ( luôn đúng )
Đúng 0
Bình luận (0)
2. a^2 + b^2 + c^2 ≥ ab + bc + ca
<=> 2a^2 + 2b^2 + 2c^2 ≥ 2ab + 2bc + 2ca
<=> 2a^2 + 2b^2 + 2c^2 - 2ab - 2bc - 2ca ≥ 0
<=> (a^2- 2ab+b^2) + (b^2-2bc+c^2) + (c^2-2ca+a^2) ≥ 0
<=> (a-b)^2 + (b-c)^2 + (c-a)^2 ≥ 0 ( luôn đúng)
Đúng 0
Bình luận (0)
CHUYÊN ĐỀ BỒI DƯỠNG HỌC SINH GIỎI VÀ NĂNG KHIẾUCâu 1. Chứng minh √7 là số vô tỉ.Câu 2.a) Chứng minh: (ac + bd)2 + (ad – bc)2 (a2 + b2)(c2 + d2)b) Chứng minh bất dẳng thức Bunhiacôpxki: (ac + bd)2 ≤ (a2 + b2)(c2 + d2)Câu 3. Cho x + y 2. Tìm giá trị nhỏ nhất của biểu thức: S x2 + y2.Câu 4.a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: b) Cho a, b, c 0. Chứng minh rằng: c) Cho a, b 0 và 3a + 5b 12. Tìm giá trị lớn nhất của tích P ab.Câu 5. Cho a + b 1. Tìm giá trị nhỏ nhất của biểu t...
Đọc tiếp
CHUYÊN ĐỀ BỒI DƯỠNG HỌC SINH GIỎI VÀ NĂNG KHIẾU
Câu 1. Chứng minh √7 là số vô tỉ.
Câu 2.
a) Chứng minh: (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
b) Chứng minh bất dẳng thức Bunhiacôpxki: (ac + bd)2 ≤ (a2 + b2)(c2 + d2)
Câu 3. Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x2 + y2.
Câu 4.
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:
b) Cho a, b, c > 0. Chứng minh rằng:
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
Câu 5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
Câu 9.
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
Câu 10. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Cau 9
(a+1)2=a2+2a+1
Mà a2+1 >hoặc=4a[Bất đẳng thức Cô-si
Suy ra 2a+4a>hoac=4a
Vay.....
Đúng 0
Bình luận (0)
Cho a,b,c,d là các số thực. Chứng minh rằng a^2+b^2>=2ab(1). Áp dụng chứng minh các bất đẳng thức sau
a) (a^2+1)(b^2+1)(c^2+1)>=8abc
b) (a^2+4)(b^2+4)(c^2+4)(d^2+4)>=256abcd
(a^2+b^2)/2>=ab
<=>(a^2+b^2)>=2ab
<=> a^2+2ab+b^2>=2ab
<=>a^2+b^2>=0(luôn đúng)
=> điều phải chứng minh.
Đúng 0
Bình luận (0)
Xét hiệu: \(a^2+b^2-2ab=\left(a-b\right)^2\ge0\)
=> \(a^2+b^2\ge2ab\)
Dấu "=" xra <=> a = b
Áp dụng ta có:
a) \(\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)\ge2a.2b.2c=8abc\)
dấu "=" xra <=> a = b = c = 1
b) \(\left(a^2+4\right)\left(b^2+4\right)\left(c^2+4\right)\left(d^2+4\right)\ge4a.4b.4c.4d=256abcd\)
Dấu "=" xra <=> a = b= c = d = 2
Đúng 0
Bình luận (0)
a) Áp dụng bđt AM-GM ta có:
\(\hept{\begin{cases}a^2+1\ge2a\\b^2+1\ge2b\\c^2+1\ge2c\end{cases}}\)
nhân theo 3 vế BDDT ta đc:
( a^2+1) (b^2+1)(c^2+1) >= 2a.2b.2c = 8abc
"=" <=> a=b=c
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau:
a2 + b2⩾1/2 với a+b ⩾1
a3+b3⩾1/4 với a+b ⩾1
Chứng minh các bất đẳng thức sau:
a2 + b2⩾1/2 với a+b ⩾1
a3+b3⩾1/4 với a+b ⩾1
1. Cho a + b 1. Tìm giá trị nhỏ nhất của biểu thức : M a3 + b3.2. Cho a3 + b3 2. Tìm giá trị lớn nhất của biểu thức : N a + b.3. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)4. Tìm liên hệ giữa các số a và b biết rằng: a b a b 5. a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4ab) Cho a, b, c 0 và abc 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 86. Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)7. Tìm các giá trị của x sao cho:a) | 2...
Đọc tiếp
1. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức : M = a3 + b3.
2. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức : N = a + b.
3. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
4. Tìm liên hệ giữa các số a và b biết rằng: a b a b
5. a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
6. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
7. Tìm các giá trị của x sao cho:
a) | 2x – 3 | = | 1 – x | b) x2 – 4x ≤ 5 c) 2x(2x – 1) ≤ 2x – 1.
8. Tìm các số a, b, c, d biết rằng : a2 + b2 + c2 + d2 = a(b + c + d)
9. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của avà b thì M đạt giá trị nhỏ nhất ? Tìm giá trị nhỏ nhất đó.
10. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. CMR giá trị nhỏ nhất của P bằng 0.
11. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau :
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....
Đúng 0
Bình luận (0)
bạn nên viết ra từng câu
Chứ để như thế này khó nhìn lắm
Đúng 0
Bình luận (0)
bạn hỏi từ từ thôi

















