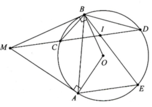
Cho (O) dây AB, M là trung điểm cung AB. 1 cát tuyến qua M cắt (O) tại C và dây AB tại D
a) Tính tổng các bán kính của các đường tròn ngoại tiếp tam giác ACD và tam giác BCD
b) Chứng minh tổng các bán kính của 2 đường tròn nói trên không đổi khi cát tuyến MC quay quanh M