Question

Cho đường tròn O bán kính R và hai điểm A, B nằm trên đường tròn (AB không là đường kính). Các tiếp tuyến tại A, B của đường tròn cắt nhau tại M. Kẻ cát tuyến MCD với đường tròn (C nằm giữa M và D)

a, Chứng minh các tam giác MBC và MDB đồng dạng

b, Chứng minh tứ giác MAOB là nội tiếp

c, Khi AB = R 3 , tính bán kinh đường tròn ngoại tiếp tứ giác MAOB theo R

d, Kẻ dây AE của (O) song song với MD. Nối BE cắt MD tại I. Chứng minh I là trung điểm của CD

Answer 1

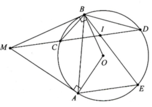
a, Vì  M B C ^ = M D B ^ = 1 2 s đ C B ⏜  nên chứng minh được ∆MBC:∆MDB (g.g)

b, Vì  M B O ^ + M A O ^ = 180 0  nên tứ giác MAOB nội tiếp

c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r =  M O 2

Gọi H là giao điểm của AB với OM

=> OH ⊥ AB; AH = BH =  R 3 2

Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R

d,  Ta có  M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và  M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2

Vì AE song song CD =>  s đ D E ⏜ = s đ A C ⏜ =>  M I B ^ = M A B ^

Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO

Từ đó ta có được  M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD