cho hàm số y= f(x)= /x-2018/+x
CMR: f(x)\(\ge\)2018 với mọi g. trị của x
Cho hàm số f(x) có đạo hàm trên ℝ thỏa mãn f’(x) – 2018f(x) = 2018.x2017.e2018x với mọi x ∈ ℝ và f(0) = 2018. Tính giá trị f(1).
A. f(1) = 2019e2018.
B. f(1) = 2018e-2018.
C. f(1) = 2018e2018.
D. f(1) = 2017e2018.
Chọn A

Lấy tích phân từ 0 đến 1 của 2 vế:
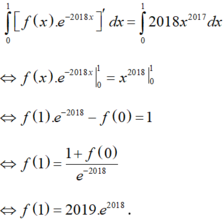
Cho hàm số f ( x ) = a x 4 + b x 2 + c với a>0, c>2018 và a+b+c<2018. Số điểm cực trị của hàm số y = f ( x ) - 2018 là
A. 1
B. 3
C. 5
D. 7
Cho hàm số f(x) thỏa mãn f(xy+1) = f(x).f(y)- f(y) -x +2 đúng với mọi số nguyên x,y bất kì. Tính giá trị 10.f(2018) + f(0)
Xét x=0,y=1 ta có f(1)=f(0)f(1)-f(1)+2 (a)
xét x=1,y=0 ta có f(1)=f(1)f(0)-f(0)+1 (b)
xét x=0,y=0 ta có f(1)=f(0)f(0)-f(0)+2 (c)
Lấy (a)-(b) suy ra f(1)=f(0)+1 thay vào (c) ta được f(0)+1=f(0)f(0)-f(0)+2 <=>f(0).f(0)-2f(0)+1=0 <=> f(0)=1 =>f(1)=f(0)+1=2
xét x=1 ta có f(y+1)=f(1)f(y)-f(y)-1+2=f(y)+1
f(y+1)=f(y)+1=f(y-1)+1+1=...F(y-n)+1+n (n là số tự nhiên)
vậy f(2018)=f(2017+1)=f(2017-2016)+1+2016( lấy n=2016)=f(1)+2017=2019
vậy biểu thức có giá trị là 10.2019+1=20191
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f ' ( x ) - 2018 f ( x ) = 2018 . 2017 . x 2017 . e 2018 x với mọi x ∈ R ; f ( 0 ) = 2018 . Giá trị của f(1) là
A. f ( 1 ) = 2018 e - 2018
B. f ( 1 ) = 2019 e - 2018
C. f ( 1 ) = 2018 e 2018
D. f ( 1 ) = 2019 e 2018
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f ' x - 2018 f x = 2018 . x 2017 . e 2018 x với mọi x ∈ R và f 0 = 2018 . Tính giá trị f(1)
A. f 1 = 2019 e 2018
B. f 1 = 2018 e - 2018
C. f 1 = 2018 e 2018
D. f 1 = 2017 e 2018
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x ) = 2 x ( x + 1 ) 2 ( x - 2018 ) 2019 : f ' ' ( x ) , ∀ x ∈ R Hàm số g ( x ) = f ' ( x ) 2019 1 - f ' ' ( x ) có bao nhiêu điểm cực trị?
A. 1
B.2
C.3
D. 4
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d với a , b , c , d ∈ ℝ , a > 0 và d > 2018 a + b + c + d - 2018 < 0 . Số cực trị của hàm số y = f ( x ) - 2018 bằng
A. 3
B. 2
C. 1
D. 5
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 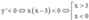 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞