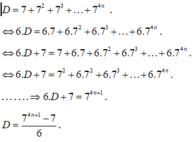CMR: 71+72+73+74+...+74n-1+74n chia hết cho 400 với n là bất kì số nguyên nào

Những câu hỏi liên quan
Chứng minh rằng
71 + 72 + 73+ 74 + ......... +74n-1 +74n chia hết cho 400
Tính tổng: D = 7 + 7 2 + 7 3 + … 7 4 n
)Cho: C = 71 + 72 + 73 + 74 + … + 72010 Chứng minh rằng C chia hết cho 8 và 57.
b) Tìm số tự nhiên x để 4x + 19 chia hết cho x + 1
b) Để 4x + 19 chia hết cho x + 1 thì 15 chia hết cho x + 1
--> x + 1 là ước của 15
TH1: x + 1 = 15 <=> x = 14
TH2: x + 1 = 1 <=> x = 0
TH3: x + 1 = 3 <=> x = 2
TH4: x + 1 = 5 <=> x= 4
Đúng 0
Bình luận (0)
CMR:
a)74n-1 chia hết cho 5
b)34n+1+2 chia hết cho 5
c)92n+1+1 chia hết cho 10
d)24n+2+1 chia hết cho 5
CMR: lập phương của 1 số nguyên n bất kì (n>1) trừ đi 13 lần số nguyên đó thì luôn chia hết cho 6.
Gọi số nguyên đó là a. Ta cần chứng minh
a3+11a⋮6a3+11a⋮6
Xét: a3+11a=a(a2+11)=a(a2−1+12)=a(a2−1)+12a=a(a+1)(a−1)+12a⋮6a3+11a=a(a2+11)=a(a2−1+12)=a(a2−1)+12a=a(a+1)(a−1)+12a⋮6
Vậy ta có đpcm.
Lời giải:
Xét biểu thức A=n3−13nA=n3−13n. Ta cần cm A⋮6A⋮6
Thật vậy: A=n3−13n=n3−n−12n=n(n2−1)−12nA=n3−13n=n3−n−12n=n(n2−1)−12n
A=n(n−1)(n+1)−12nA=n(n−1)(n+1)−12n
Vì n,n−1n,n−1 là hai số tự nhiên liên tiếp nên tích n(n−1)⋮2n(n−1)⋮2
⇒n(n−1)(n+1)⋮3⇒n(n−1)(n+1)⋮3
Vì n−1,n,n+1n−1,n,n+1 là ba số tự nhiên liên tiếp nên tích n(n−1)(n+1)⋮3n(n−1)(n+1)⋮3
Kết hợp với (2,3) nguyên tố cùng nhau, do đó: n(n−1)(n+1)⋮6n(n−1)(n+1)⋮6
Mà 12n⋮612n⋮6
⇒A=n(n−1)(n+1)−12n⋮6⇔n3−13n⋮6⇒A=n(n−1)(n+1)−12n⋮6⇔n3−13n⋮6
Ta có đpcm.
Ta phải chứng minh: \(A\left(n\right)=n^3-13n⋮6\)
Chú ý rằng: \(13n=12n+n\), mà \(12n⋮6\), ta biến đổi A(n) thành:
\(A\left(n\right)=\left(n^3-n\right)-12n\)
Ta có: \(n^3-n=n\left(n^2-1\right)=\left(n-1\right)n\left(n+1\right)\)
Đây là tích của 3 số nguyên liên tiếp, tích này luôn chia hết cho 6. A(n) là hiệu của 2 hạng tử: \(n^3-n\)và 12n, mỗi hạng tử chia hết cho 6, nên \(A\left(n\right)⋮6\left(đpcm\right)\)
Bài 1: a, Chứng minh: A21+22+23+24+...+22010 chia hết cho 3 và 7 b, Chứng minh: B31+32+33+34+...+22010 chia hết cho 4 và 13 c, Chứng minh: C51+52+53+54+...+52010 chia hết cho 6 và 31 d, Chứng minh: C71+72+73+74+...+72010 chia hết cho 8 và 57Bài 2: So sánha, A20+21+22+23+...+22011 và B22011-1b, A2019.2021 và B20202
Đọc tiếp
Bài 1: a, Chứng minh: A=21+22+23+24+...+22010 chia hết cho 3 và 7
b, Chứng minh: B=31+32+33+34+...+22010 chia hết cho 4 và 13
c, Chứng minh: C=51+52+53+54+...+52010 chia hết cho 6 và 31
d, Chứng minh: C=71+72+73+74+...+72010 chia hết cho 8 và 57
Bài 2: So sánh
a, A=20+21+22+23+...+22011 và B=22011-1
b, A=2019.2021 và B=20202
Bài 1:
\(a,A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\\ A=\left(1+2\right)\left(2+2^3+...+2^{2009}\right)=3\left(2+...+2^{2009}\right)⋮3\\ A=\left(2+2^2+2^3\right)+...+\left(2^{2008}+2^{2009}+2^{2010}\right)\\ A=\left(1+2+2^2\right)\left(2+...+2^{2008}\right)=7\left(2+...+2^{2008}\right)⋮7\)
\(b,\left(\text{sửa lại đề}\right)B=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\\ B=\left(1+3\right)\left(3+3^3+...+3^{2009}\right)=4\left(3+3^3+...+3^{2009}\right)⋮4\\ B=\left(3+3^2+3^3\right)+...+\left(3^{2008}+3^{2009}+3^{2010}\right)\\ B=\left(1+3+3^2\right)\left(3+...+3^{2008}\right)=13\left(3+...+3^{2008}\right)⋮13\)
Đúng 3
Bình luận (0)
Bài 2:
\(a,\Rightarrow2A=2+2^2+...+2^{2012}\\ \Rightarrow2A-A=2+2^2+...+2^{2012}-1-2-2^2-...-2^{2011}\\ \Rightarrow A=2^{2012}-1>2^{2011}-1=B\\ b,A=\left(2020-1\right)\left(2020+1\right)=2020^2-2020+2020-1=2020^2-1< B\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
chung minh rang moi so n de: a) 74n - 1 chia het cho 5
b) 34n + 1 + 2 chia het cho 5
c) 24n + 1 + 3 chia het cho 5
d) 92n + 1 + 1 chia het cho 10
viết lại đề cho chuẩn
nhìn mình chẳng hiểu n là số mũ hay là nhân, hay có gạch trên đầu...
Đúng 0
Bình luận (0)
a)
\(74^n-1\) đề sai vơi n lẻ không chia hết cho 5 xem lại và viết cho chuẩn đi
Đúng 0
Bình luận (0)
Cmr 20+21+22+.....25n-2+25n-1 chia hết cho 31 nếu n là số nguyên dương bất kì
B = 74 - 73 + 72 - 71 +.................+2 - 1
B = 74 - 73 + 72 - 71 +.................+2 - 1
B = 1 + 1 + ... + 1
mà có 37 số 1
B = 1 x 37
=> B = 37
Đúng 0
Bình luận (0)