\(\text{Chứng minh rằng trong một bình thang cân; bình phương của đường chéo bằng bình phương cạnh bên cộng với tích hai đáy}\)
\(\text{(Đề thi HSG Toán 8 huyện Gia Viễn - Tỉnh Ninh Bình)}\)
Mong thầy cô và các bạn giúp đỡ !!!!!
Chứng minh rằng trong hình thang cân đường trung bình của hình thang luôn bé hơn đường chéo của nó
Chứng minh rằng hình chữ nhật ABCD trên hình 84 cũng là một hình bình hành, một hình thang cân.
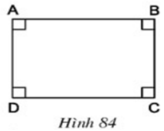
- ABCD có các góc đối bằng nhau (đều là góc vuông) nên ABCD là hình bình hành
- ABCD là hình thang (vì AB // CD),
hai góc ở đáy: góc D = góc C ⇒ ABCD là hình thang cân
Cho hình thang cân ABCD, đáy nhỏ AB. đg cao BH bằng đường trung bình hình thang ABCD. Chứng minh rằng BD vuông góc với AC?
Giải hộ mình với mai mình thi học sinh giỏi rùi!
Chứng minh rằng nếu một tứ giác có tâm đối xứng thì đó là hình bình hành. (đừng nhầm với hình thang cân nha vì hình thang cân không có tâm đối xứng đâu)
cho hình thang cân abcd(ab//cd).gọi o là giao của ac và bd :
a) chứng minh tam giác cod cân
b) chứng minh rằng nếu hai đường chéo ac và bd của hình thang cân vuông góc với nhau thì (ab+cd)^2=2.ac^2
Không đc dùng đường trung bình nhé
Chứng minh rằng hình thang có 2 góc kề một đáy bằng nhau là hình thang cân
Chứng minh rằng mọi hình thang cân nội tiếp được trong 1 đường tròn và giao điểm 2 đường chéo thuộc trục đối xứng của hình thang cân.
gia điểm 2 đường chéo luôn thuộc trục đối xúng của hình thang cân ạ.
Bạn hạ vuông góc xuống 2 đáy là đc
Cho hình bình hành ABCD, hai đường chéo không vuông góc với nhau. Vẽ điểm
E đối xứng với A qua BD. Chứng minh rằng 4 điểm B,C,E,D là 4 đỉnh của một hình
thang cân.