Cho đường tròn tâm O có 2 dây AB // CD . Chứng minh cung AC = cung BD.
Những câu hỏi liên quan
Cho đường tròn tâm (O) và dây AB, lấy 2 điểm M,N nằm trên cung nhỏ AB chia cung này thành 3 cung bang nhau là Cung AM=Cung MN=Cung NB. Các bán kính OM và ON cắt AB tại C và D. Chứng minh rằng:
a. AC=BD
b. AC > CD
Cho đường tròn tâm (O) và dây AB, lấy 2 điểm M,N nằm trên cung nhỏ AB chia cung này thành 3 cung bang nhau là Cung AM=Cung MN=Cung NB. Các bán kính OM và ON cắt AB tại C và D. Chứng minh rằng:
a. AC=BD
b. AC > CD
Cho đường tròn tâm (O) và dây AB, lấy 2 điểm M,N nằm trên cung nhỏ AB chia cung này thành 3 cung bang nhau là Cung AM=Cung MN=Cung NB. Các bán kính OM và ON cắt AB tại C và D. Chứng minh rằng:
a. AC=BD
b. AC > CD
cho Ac là một dây khác đường kính của đường tròn tâm O B là một điểm trên cung nhỏ AC sao cho AB nhỏ hơn BC kẻ dây BD của đường tròn tâm O và vuông góc với AC tại H kẻ BI vuông góc với CD kẻ BK vuông góc với AD chứng minh HIK thẳng hàng
góc DCA=góc DBA
góc AKB=góc AHB=90 độ
=>AHBK nội tiếp
=>góc AKB+góc AHB=180 độ
=>góc AKH=góc ABH=góc HCD
góc DAC=góc DBC=góc DIH
=>180 độ-góc DAC=180 độ-góc DIH
=>góc CAK=góc HIC
=>góc HAK=góc HIC
mà góc AKH=góc HCI
nên ΔHAK đồng dạng với ΔHIC
=>góc AHK=góc IHC
=>góc IHC+góc KHC=180 độ
=>góc KHI=180 độ
=>K,I,H thẳng hàng
Đúng 1
Bình luận (2)
Cho đường tròn tâm O, đường kính AB. Ke dây cung CD (C thuộc cung AD). AC cắt BD tại M , AD cắt BC tại H.
a, Chứng minh : H là trực tâm của tam giác MAB.
MH cắt AB tại K.Chứng minh 4 điểm K, H, D, B thuộc một đường tròn.
Giả sử AB là một dây cung của đường tròn (O). Trên cung nhỏ AB lấy các điểm C và D sao cho A C ⏜ = B D ⏜ . Chứng minh AB và CD song song
Ta lấy K là điểm chính giữa cung nhỏ A B ⏜
Ta chứng minh được C K ⏜ = K D ⏜
Từ đó ta có OK ⊥ CD, OK ⊥ AB => CD//AB
Đúng 1
Bình luận (0)
Cho đương tròn(O, R), dây AB cố định không đi qua tâm. C là điểm nằm trên cung nhỏ AB sao cho cung AC không lớn hơn cung BC. Kẻ dây CD vuông góc với AB tại H. Gọi điểm K là hình chiếu vuông góc của C trên đường thẳng DA.a) Chứng minh: Bốn điểm A, H, C, K cùng thuộc một đường tròn.b) Chứng minh: CD là tia phân giác của góc BCKc) KH cắt BD tại E. Chứng minh: CE vuông góc BDd) Khi điểm C di chuyển trên cung nhỏ AB. Xác định vị trí của điểm C để CK. AB + CE. DB có giá trị lớn nhất?
Đọc tiếp
Cho đương tròn(O, R), dây AB cố định không đi qua tâm. C là điểm nằm trên cung nhỏ AB sao cho cung AC không lớn hơn cung BC. Kẻ dây CD vuông góc với AB tại H. Gọi điểm K là hình chiếu vuông góc của C trên đường thẳng DA.
a) Chứng minh: Bốn điểm A, H, C, K cùng thuộc một đường tròn.
b) Chứng minh: CD là tia phân giác của góc BCK
c) KH cắt BD tại E. Chứng minh: CE vuông góc BD
d) Khi điểm C di chuyển trên cung nhỏ AB. Xác định vị trí của điểm C để CK. AB + CE. DB có giá trị lớn nhất?
a, Xét tứ giác AKCH có: \(\widehat{AKC}+\widehat{AHC}=90+90=180\)=> tứ gác AKCH nội tiếp
b,Tứ giác AKCH nội tiếp => \(\widehat{HCK}=\widehat{HAD}\)(góc trong và góc ngoài đỉnh đối diện)
Mặt khác: \(\widehat{HAD}=\widehat{BCD}=\frac{1}{2}sđ\widebat{BD}\)
=> \(\widehat{BCD}=\widehat{ACD}\)=> CD là phân giác \(\widehat{KCB}\)
c, Tứ giác AKCH nội tiếp: => \(\widehat{CKE}=\widehat{CAH}\)
Mà: \(\widehat{CDB}=\widehat{CAH}=\frac{1}{2}sđ\widebat{BC}\)
=> \(\widehat{CKE}=\widehat{CDE}\)=> tứ giác CKDE nội tiếp
=> \(\widehat{CKD}+\widehat{CED}=180\Rightarrow\widehat{CED}=180-\widehat{CKD}=180-90=90\)
=> \(CE⊥BD\)(ĐPCM)
d, em xem lại xem có gõ sai đề không nhé
Đúng 0
Bình luận (0)
Câu d) Khi C di chuyển trên cung nhỏ̉ AB. Xác định vị trí C để CK.AD+CE.DB có giá trị lớn nhất.
Nhờ mọi người giải dùm e với.
Đúng 0
Bình luận (0)
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD R (C thuộc cung AD). Nối AC và BD cắt nhau tại Ma, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc
A
M
B
^
không đổib, Cho
A
B
C
^
30...
Đọc tiếp
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD = R (C thuộc cung AD). Nối AC và BD cắt nhau tại M
a, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc A M B ^ không đổi
b, Cho A B C ^ = 30 0 , tính độ dài cung nhỏ AC và diện tích hình viên phân giói hạn bởi dây AC và cung nhỏ AC
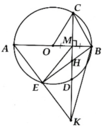
a, Chứng minh được ∆COD đều => A M B ^ = 60 0
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3
Đúng 0
Bình luận (0)
Cho nửa đường tròn (O) có đường kính AB = 2R. CD là dây cung thay đổi của nửa đường tròn sao cho CD = R và C thuộc cung AD (C khác A và D khác B). AD cắt BC tại H, hai đường thẳng AC và BD cắt nhau tại F.
a) Chứng minh tứ giác CFDH nội tiếp
b) Chứng minh CF.CA = CH.CB
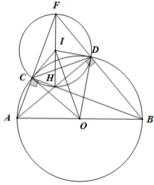
a) Vì C, D thuộc nửa đường tròn đường kính AB nên
A C B = A D B = 90 o ⇒ F C H = F D H = 90 o ⇒ F C H + F D H = 180 o
Suy ra tứ giác CHDF nội tiếp
b) Vì AH ⊥ BF, BH ⊥ AF nên H là trực tâm ∆ AFB ⇒ FH ⊥ AB
⇒ C F H = C B A ( = 90 o − C A B ) ⇒ Δ C F H ~ Δ C B A ( g . g ) ⇒ C F C B = C H C A ⇒ C F . C A = C H . C B
Đúng 1
Bình luận (0)