rút gọn biểu thức
-3a-{-(-4a+5)+[-(5-6a)+(-12-4a)]}
Rút gọn biểu thức:
D=-3a-{-(-4a+5)+[-(5-6a)+(-12-4a)]}
E=-(2a+4)-{[-2a-(4-10a)+(5a-3)]-(-12+3a)
Rút gọn các biểu thức sau
b) 7a.(3a-5)+(2a-3)(4a+1)-(6a-2)2
\(7a\left(3a-5\right)+\left(2a-3\right)\left(4a+1\right)-\left(6a-2\right)^2\)
\(=21a^2-35a+8a^2+2a-12a-3-36a^2+24a-4\)
\(=-7a^2+4a-7\)
Cho số thực dương a. Rút gọn biểu thức 4 a - 9 a - 1 2 a 1 2 - 3 a - 1 2 + a - 4 + 3 a - 1 a 1 2 - a - 1 2
A. 9 a 1 2
B. 9a
C. 3a
D. 3 a 1 2
4
a
-
9
a
-
1
2
a
1
2
-
3
a
-
1
2
+
a
-
4
+
3
a
-
1
a
1
2
-
a
-
1
2
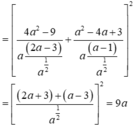
Chọn B
Rút gọn các biểu thức sau
a) \(\sqrt{25a^2}+3a\) với a ≥ 0
b) \(\sqrt{9a^4}+3a^2\)
c) \(5\sqrt{4a^6}-3a^3\) với a < 0
a) \(=5\left|a\right|+3a=5a+3a=8a\)
b) \(=3\left|a^2\right|+3a^2=3a^2+3a^2=6a^2\)
c) \(=5.2\left|a^3\right|-3a^3=-10a^3-3a^3=-13a^3\)
Rút gọn cái biểu thức sau
1) 5√4a^6 -3a^3 với a<0
2)√9a^4 +3a^2
3) √x^2-10x+25 phần x-5
cho mik hỏi là dấu căn bậc 2 là của mik số 4 hay là cả 4a^6 và các phần kia cug vậy
Rút gọn biểu thức P = a - 3 - 4 a - 1 a 1 2 - 4 a - 1 2 - 1 a - 1 2 với a là một số thực dương
A. P = a
B. P = a - 1 2
C. P = a - 1
D. P = a 1 2
Đáp án B
P = a − 3 − 4 a − 1 a 1 2 − 4 a − 1 2 − 1 a − 1 2 = a 1 2 − 3 a − 1 2 − 4 a − 3 2 − a 1 2 + 4 a − 1 2 a − 1 2 ( a 1 2 − 4 a − 1 2 ) = a − 1 2 − 4 a − 3 2 1 − 4 a − 1 = a − 1 2
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
\(\frac{1}{3}\sqrt{9+6a+a^2}+\frac{4a}{3}+5\)
Rút gọn biểu thức bằng cách đua thừa số ra ngoài dấu căn
giúp mk vs !
\(\frac{1}{3}\sqrt{9+6a+a^2}+\frac{4a}{3}+5\)
\(=\frac{1}{3}\sqrt{\left(a+3\right)^2}+\frac{4a}{3}+5\)
\(=\frac{1}{3}\left|a+3\right|+\frac{4a}{3}+5\)(1)
Với a < 3 \(\left(1\right)=-\frac{1}{3}\left(a+3\right)+\frac{4}{3}a+5=a+4\)
Với a >= 3 \(\left(1\right)=\frac{1}{3}\left(a+3\right)+\frac{4}{3}a+5=\frac{5}{3}a+6\)
hãy rút gọn các biểu thức sau
\(a.5\sqrt{4a^6}-3a^3v\text{ới}a< 0\)
b.\(\sqrt{9a^4}+3a^2\)
c.\(\frac{\sqrt{x^2-10x+25}}{x-5}\)
\(a,5\sqrt{4a^6}-3a^3=5\left|2a^3\right|-3a^2=-10a^3-3a^3=-13a^3\)(vì a<0)
b)\(\sqrt{9a^4}+3a^2=\left|3a^2\right|+3a^2=3a^2+3a^2=6a^2\)
c)\(\frac{\sqrt{x^2-10x+25}}{x-5}=\frac{\left|x-5\right|}{x-5}\)
Với x-5>0 => x>5 => \(\frac{\sqrt{x^2-10x+25}}{x-5}=1\)
Với x-5<0=>x<5 =>\(\frac{\sqrt{x^2-10x+25}}{x-5}=-1\)