Cho hình vuông ABCD . Gọi M,N,P lần lượt là trung điểm của AD,BC,DC . Đường thẳng AP và đường thẳng DN cắt nhau tại K
a> Chứng minh tứ giác BMDN là hình bình hành
b> Chứng minh AP vuông góc với DN
c> Chứng minh tứ giác BMKN là hình thang cân
d> Cho AB=\(\sqrt{5}\)cm . Tính diện tích tam giác MDK
PS : Các bạn giúp mình với , mình đang cần giải gấp lắm ạ :((((

Những câu hỏi liên quan
Cho hình vuông ABCD. Gọi M,N,P lần lượt là trung điểm của AD, BC,DC. Đường thẳng AP và đường thẳng DN cắt nhau tại K
a) CM: tứ giác BMDN là hình bình hành
b) CM: AP vuông góc với DN
c) CM: tứ giác BMKN là hình thang cân
d) Cho AB=√5. Tính diện tích tam giác MDK
Cho hình bình hành ABCD. Gọi M và N lần lượt là trung điểm của AD và BC. Đường chéo AC cắt các đoạn thẳng BM và DN theo thứ tự tại E và K.
a) Chứng minh tứ giác BMDN là hình bình hành.
b) Chứng minh AE = EK = KC.
c) Gọi I là trung điểm của BE. Chứng minh tứ giác AIKM là hình bình hành
a: Xét tứ giác BMDN có
DM//BN
DM=BN
Do đó: BMDN là hình bình hành
Đúng 0
Bình luận (0)
Cho hình vuông ABCD.Gọi M,N,P lần lượt là trung điểm của AD,BC,DC.Đường thẳng AP và đường thẳng DN cắt nhau tại K.
a)C/m tứ giác BMDN là hình bình hành.
b)C/m AP vuông góc với DN
c)C/m tứ giác BMKN là hình thang cân.
d)Cho AB=\(\sqrt{5cm}\) .Tính diện tích tam giác MDK
Câu a,b,clàm được rồi,mấy bạn giúp mình câuu d thôi nha
a) Ta có DM song song và bằng BN nên BMDN là hình bình hành (vì có 2 cạnh đối song song và bằng nhau)
b) Tam giác CDN bằng tam giác DAP (cạnh - góc - cạnh)
=> Góc D1 = góc A1
Ta lại có Góc D2 + Góc D1 = Góc D = 90 độ
=> Góc D2 + Góc A1 = 90 đo
Trong tam giác KAD có tổng 2 góc A và D bằng 90 độ nên góc K bằng 90 độ
=> AP vuông góc với DN
c) Tương tự câu b ta có BM vuông góc với AP
=> BM // DN (vì cùng vuông góc vời AP)
=> BMKN là hình thang.
Theo câu b tam giác KAD vuông tại K có KM là trung tuyến ứng với cạnh huyền => KM = 1/2 AD
=> KM = BN
=> BMKN là hình thang cân
d) \(DP=\frac{1}{2}\sqrt{5},AP=\sqrt{5-\frac{1}{4}5}=\frac{\sqrt{15}}{2}\)
\(DP^2=PK.PA\)
=> \(PK=\frac{DP^2}{PA}=\frac{\frac{5}{4}}{\frac{\sqrt{15}}{2}}=\frac{\sqrt{15}}{6}\)
=> \(\frac{PK}{PA}=\frac{\frac{\sqrt{15}}{6}}{\frac{\sqrt{15}}{2}}=\frac{1}{3}\)
=> Đường cao hạ từ K xuống DC bằng 1/3 đường cao hạ từ A xuống DC
=> Đường cao hạ từ K xuống DC = \(\frac{1}{3}\sqrt{5}\)
=> Đường cao hạ từ K xuống MN bằng \(\frac{1}{2}\sqrt{5}-\frac{1}{3}\sqrt{5}=\frac{\sqrt{5}}{6}\)
=> Diện tích KMN bằng \(\frac{1}{2}.MN.KH_2=\frac{1}{2}\sqrt{5}\frac{\sqrt{5}}{6}=\frac{5}{12}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có diện tích S. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Đường thẳng BQ cắt AP tại E và cắt MC tại F. Đường thẳng DN cắt AP tại S và cắt MC tại R.
a) Chứng minh tứ giác EFRS là hình bình hành.
b) Tính diện tích hình bình hành EFRS theo S.
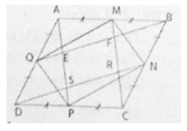
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Gọi M,N,P lần lượt là trung điểm của AD,BC,DC. Đường thẳng AP và DN cắt nhau tại K
a. CM: BMDN là hình bình hành
b. CM: AP\(\perp\)DN
c. CM:BMKN là hình thang cân
d. Cho AB =\(\sqrt{5}\)cm. Tính diện tích tam giác MDK.
Giúp mk nha!!
https://olm.vn/hoi-dap/detail/96788252350.html
Tham khảo ở link này (mình gửi cho)
Hoc tốt!!!!!!!!!!!!
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. Các đường thẳng BM, DN cắt đường chéo AC tại P, Q.
a) Chứng minh AP = PQ = QC
b) Tứ giác MPNQ là hình gì?
c) Xác định tỉ số CA / CD để MPNQ là hình chữ nhật
Giúp mình phần C với ạ
Lời giải :
Để \(MPNQ\) là hình chữ nhật thì \(MN=PQ\)
Ta có : \(AM=\dfrac{1}{2}AD=\dfrac{1}{2}BC=BN\) , \(AM\) song song với BN \(\Rightarrow AMNB\) là hình bình hành \(\Rightarrow AB=MN\Rightarrow MN=CD\)
Ta lại có : \(AP=PQ=QC\) ( cmt ) \(\Rightarrow PQ=\dfrac{1}{3}AC\)
\(\Rightarrow CD=MN=PQ=\dfrac{1}{3}AC\)
\(\dfrac{CA}{CD}=3\) thì MPNQ là hình chữ nhật
Đúng 2
Bình luận (0)
cho hcn ABCD ;AB2AD. trên cạnh AD lấy M ,trên cạnh BC lấy P sao cho AMCP .kẻ BH vuông góc vs AC tại H .gọi Q là trung điểm của CH ,đường thẳng kẻ qua P song song vs MQ cắt AC tại Na) chứng minh tứ giác MNPQ là hình bình hànhb) khi M là trung điểm AD .chứng minh BQ vuông góc vs NP c) đường thẳng AP cắt DC tại điểm F . chứng minh rằng frac{1}{AB^2}frac{1}{AP^2}+frac{1}{4AF^2}
Đọc tiếp
cho hcn ABCD ;AB=2AD. trên cạnh AD lấy M ,trên cạnh BC lấy P sao cho AM=CP .kẻ BH vuông góc vs AC tại H .gọi Q là trung điểm của CH ,đường thẳng kẻ qua P song song vs MQ cắt AC tại N
a) chứng minh tứ giác MNPQ là hình bình hành
b) khi M là trung điểm AD .chứng minh BQ vuông góc vs NP
c) đường thẳng AP cắt DC tại điểm F . chứng minh rằng \(\frac{1}{AB^2}=\frac{1}{AP^2}+\frac{1}{4AF^2}\)
Cho tam giác ABC vuông tại C. Gọi M, N lần lượt là trung điểm của cạnh BC và AB. Gọi P là điểm đối xứng của M qua N.
a) Chứng minh tứ giác MBPA là hình bình hành
b) Chứng minh tứ giác PACM là hình chữ nhật
c) Đường thẳng CN cắt PB tại Q. Chứng minh BQ = 2 PQ
mọi người vẽ hình giúp em với
a: Xét tứ giác MBPA có
N là trung điểm của MP
N là trung điểm của BA
Do đó: MBPA là hình bình hành
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD (ABAD). Trên cạnh AD,BC lần lượt lấy các điểm M, N sao cho AMCNA) CHỨNG MINH RẰNG BM//DNB) Gọi O là trung điểm của BD. CHỨNG MINH AC, BD, MN đồng quy tại OC) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CHỨNG MINH: Tứ giác PBQD là hình thoiD) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CHỨNG MINH: Tứ giác OBKQ là hình chữ nhật và BC _|_(vuông góc ) OK
Đọc tiếp
Cho hình chữ nhật ABCD (AB>AD). Trên cạnh AD,BC lần lượt lấy các điểm M, N sao cho AM=CN
A) CHỨNG MINH RẰNG BM//DN
B) Gọi O là trung điểm của BD. CHỨNG MINH AC, BD, MN đồng quy tại O
C) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CHỨNG MINH: Tứ giác PBQD là hình thoi
D) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CHỨNG MINH: Tứ giác OBKQ là hình chữ nhật và BC _|_(vuông góc ) OK

















